Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
 Дано:
Дано:
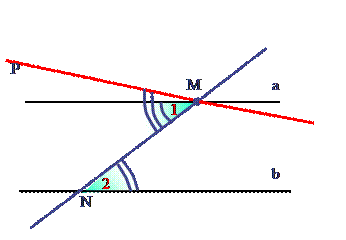
а || b, MN - секущая.
Доказать:
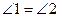 (НЛУ)
(НЛУ)
Доказательство: (способ от противного)
Допустим, что 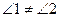 .
.
Отложим от луча МN угол NМР, равный углу 2.
По построению накрест лежащие углы 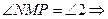 РМ || b.
РМ || b.
Получили, что через точку М проходит две прямые (а и МР), параллельные прямой b!!! Это противоречит аксиоме параллельных прямых. Значит наше допущение неверно!!! 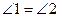 .
.
Следствие
Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.
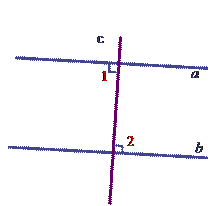
Дано:
а || b.
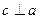
Доказать:
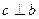
Доказательство:
Прямая с пересекает прямую а, поэтому она пересекает также прямую b. При пересечении параллельных прямых а и b секущей с образуются равные накрест лежащие углы: 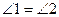 . Так как
. Так как 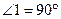 , то и
, то и 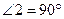 , т.е.
, т.е. 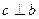 , что и требовалось доказать.
, что и требовалось доказать.
Если две параллельные прямые пересечены секущей, то соответственные углы равны.
 Дано:
Дано:
а || b, с - секущая.
Доказать:
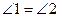 (СУ)
(СУ)
Доказательство:
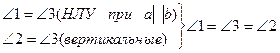
Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 1800.
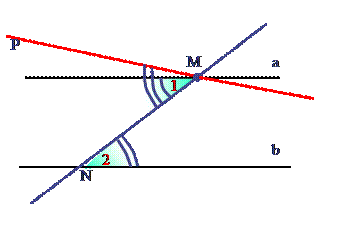
Дано:
а || b, с - секущая.
Доказать:
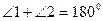 (ОУ)
(ОУ)
Доказательство:
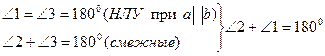 .
.
 2015-04-12
2015-04-12 1540
1540
