Внешний угол треугольник

Если в треугольнике все углы острые, то треугольник прямоугольный.

Если в треугольнике один угол тупой, то треугольник тупоугольный.

Если в треугольнике один угол прямой (90⁰), то треугольник прямоугольный.

Внешний угол – это угол треугольника, смежный с каким-нибудь углом этого треугольника.

Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

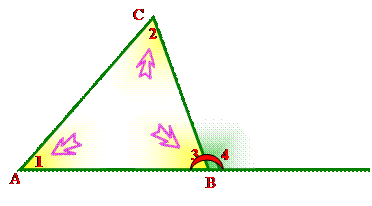Дано: Δ АВС

Доказать: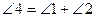

Доказательство:

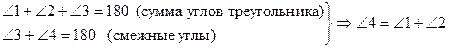
В треугольнике против большей стороны лежит больший угол.

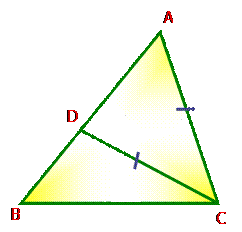Дано:

Δ АВС

АВ > АС

Доказать:

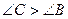
Доказательство:

отложим на АВ отрезок АD: АD = АС.

так как АD < АВ 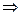D лежит между А и В.

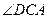часть угла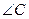

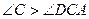
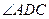- внешний угол Δ СВD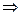

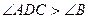
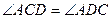(Δ АСD - равнобедренный)

.

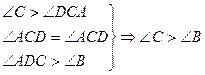Против большего угла лежит большая сторона

Дано:

Δ АВС

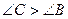
Доказать:

АВ > АС

Доказательство: (от противного)

либо АВ = АС, либо АС < АВ.

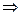
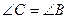
1) треугольник АВС – равнобедренный 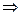противоречит условие.

2) АС < АВ 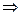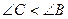(против большей стороны лежит больший угол) 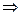противоречит условие.

предположение неверно 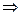АВ > АС

Следствие 1

В прямоугольном треугольнике гипотенуза больше катета.

Доказательство:

Гипотенуза лежит против прямого угла, а катет – против острого. Так как прямой угол больше острого, то гипотенуза больше катета.

Следствие 2 (признак равнобедренного треугольника)

Если два угла треугольника равны, то треугольник равнобедренный

Доказательство: (от противного)

предположим АВ > ВС 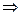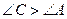противоречит условию Δ АВС – равнобедренный.

Каждая сторона треугольника меньше суммы двух других сторон.

Дано:

Δ АВС

Доказать:

АВ < АС + СВ

Доказательство:

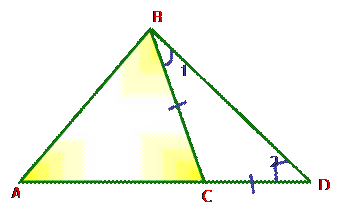
отложим на продолжении АС: СD = СВ

Δ ВСD – равнобедренный

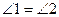
ΔАВD: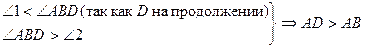

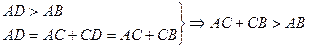
Следствие

Для любых трех точек А, В и С, не лежащих на одной прямой, справедливы неравенства: АВ < АС + СВ, АС < АВ + ВС, ВС < ВА + АС.