Решение. Ра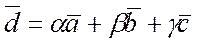венство (1) называется разложением вектора по векторам [1]

Равенство (1) называется разложением вектора 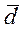по векторам 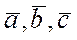[1]. Нас интересует такие системы векторов, по которым разложение любого вектора пространства возможно и притом единственным образом. Такой системой векторов в пространстве служит любая тройка некомпланарных векторов 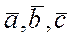, которые называются базисом пространства, а коэффициенты разложения вектора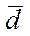 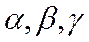- координатами вектора в этом базисе.

Покажем, что векторы 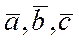образуют базис. Смешанное произведение некомпланарных векторов отлично от нуля [1].

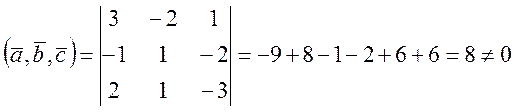
Итак, векторы 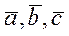образуют базис.

Найдем координаты вектора 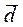в этом базисе. Равенство (1) равносильно системе линейных уравнений с тремя неизвестными :

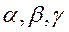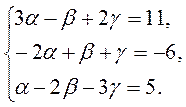
Решим ее по правилу Крамера [10]:

, , .

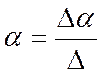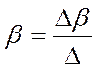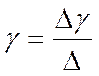Вычислим определитель системы линейных уравнений, который составлен из коэффициентов при неизвестных:

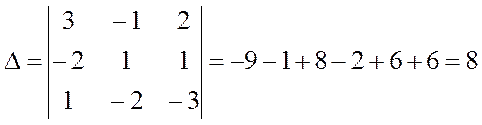
Вычислим вспомогательные определители 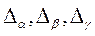, которые получаются из определителя системы путем замены столбца коэффициентов при соответствующей неизвестной столбцом свободных членов:

,

,

,

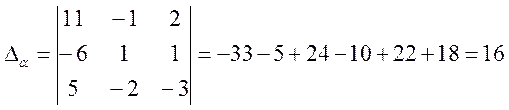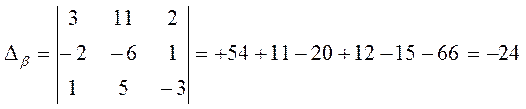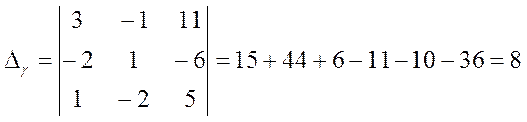Решение системы имеет вид:

; ; .

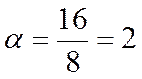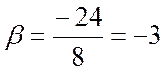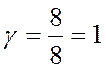Итак, вектор 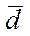в базисе 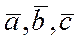представим в виде:

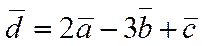, т.е. имеем координаты (2;-3;1).