2015-04-12
855
Для совместности системы необходимо и достаточно, чтобы ранг матрицы системы равнялся рангу расширенной матрицы этой системы (теорема Кронекера – Капелли) [1]. Матрица А системы состоит из коэффициентов при неизвестных
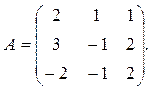
Если к матрице системы добавить столбец из свободных членов, то получим расширенную матрицу системы
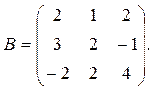
Под рангом понимается наибольший порядок минора, отличного от нуля. Для матрицы А минором наивысшего порядка, равного трем, является ее определитель [3]:
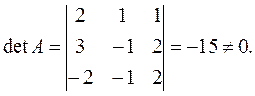Следовательно, 
.
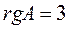В матрице В нет минора порядка больше 3, а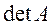 
является одним из ее миноров третьего порядка, поэтому 
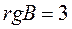.Система совместна, так как 
.
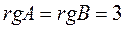а) Решение методом Гаусса состоит в преобразовании системы к треугольному виду, что достигается исключением неизвестных х1 из 2-го и 3-го уравнений и х2 – из 3-го уравнения. Последовательное исключение неизвестных осуществляется с помощью элементарных преобразований системы, приводящих к равносильной системе, к которым относятся [1]:
1) перестановка любых двух уравнений;
2) умножение обеих частей одного уравнения на любое отличное от нуля число;
3) прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на любое число.
Все преобразования, связанные с последовательным исключением неизвестных, удобнее применять не к самой системе линейных уравнений, а к ее расширенной матрице. Получающиеся при этом матрицы называются эквивалентными и соединяются знаком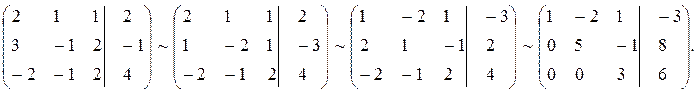 
(вертикальной чертой отделены элементы матрицы А).
Были проведены следующие действия:
1) из элементов второй строчки вычли элементы первой строки;
2) первую и вторую строки поменяли местами;
3) к элементам второй строки прибавили соответствующие элементы первой строки, умноженные на (-2);
4) к элементам третьей строки прибавили соответствующие элемент второй строки.
Полученной матрице соответствует система уравнений:
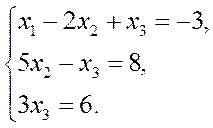
Решая уравнения снизу вверх, имеем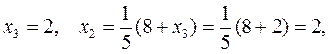 
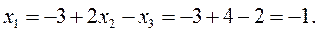
Ответ: (-1, 2, 2).
б) Для решения системы матричным методом вводим матрицы
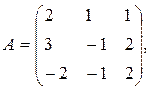
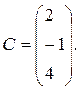
Тогда эта система запишется в виде матричного уравнения АХ=С [13].
Умножив левую и правую части уравнения на А-1 слева, получим
А-1АХ=А-1С,где А-1 – обратная матрица.
Так как А-1А=Е, то Х=А-1С.
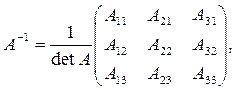где
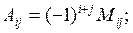
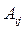- алгебраическое дополнение, соответствующее элементу 
;
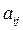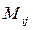- минор (определитель), который получается из матрицы А после вычеркивания i-ой строки и j-го столбца.
Найдем алгебраические дополнения:
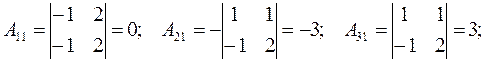
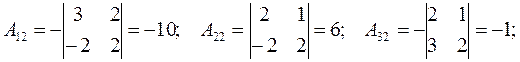
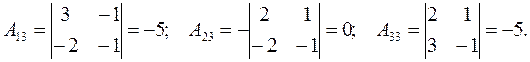
Cледовательно:
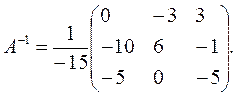
Пользуясь правилом умножения матриц получим решение системы [10]:
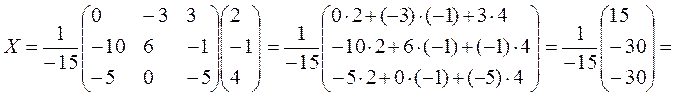
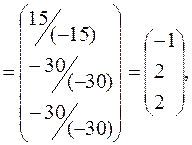
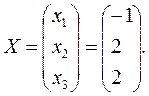
откуда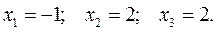 
Сравните ответы, полученные при решении системы методом Гаусса и матричным методом.
