Решение. 1) Комплексными называются числа вида z=x+iy, где x и y – действительные числа, а - мнимая единица

1) Комплексными называются числа вида z=x+iy, где x и y – действительные числа, а 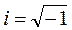- мнимая единица. Числа x и y называются соответственно действительной и мнимой частями комплексного числа Z. Число z=x-iy называется сопряженным числу z=x+iy. С геометрической точки зрения числу Z можно сопоставить вектор, направленный из начала координат в точку Z с координатами x и y [7]. Длина этого вектора называется модулем комплексного числа и определяется равенством

.

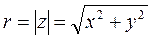Угол, образованный вектором Z с положительным направлением оси ОХ, называется аргументом числа Z и обозначается Argz. Для аргумента j справедливы формулы [7]:

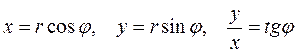
значения Argz определяются не однозначно, а с точностью до слагаемого 2kp (k=0; ±1; ±2; …). Argz=аrgz+2kp, где аrgz – главное значение аргумента,

.

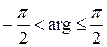Тригонометрическая форма комплексного числа z=x+iy имеет вид [7]

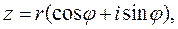где

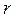- модуль комплексного числа,

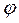- главное значение его аргумента.

Данное число 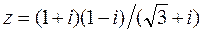запишем в алгебраической форме. Для этого в числителе раскроем скобки и умножим числитель и знаменатель на число сопряженное знаменателю. Получим:

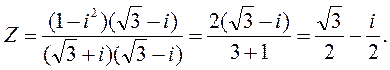
Чтобы число 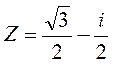записать в тригонометрической форме, найдем его модуль и главное значение аргумента:

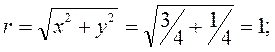
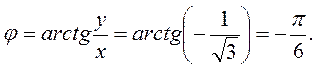
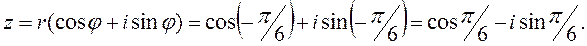
2) Решим уравнение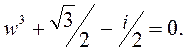

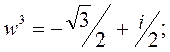
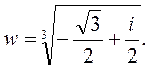
Чтобы найти все корни n-ой степени из числа Z, воспользуемся формулой [9]:

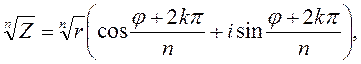
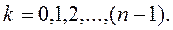
Для числа 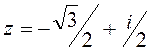найдем модуль и аргумент.

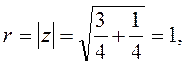
т.к. 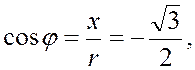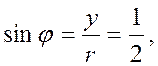то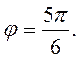

Итак:

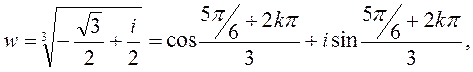
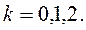
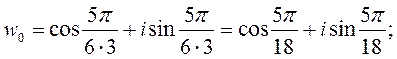
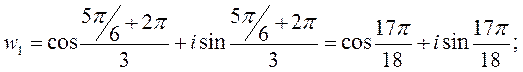
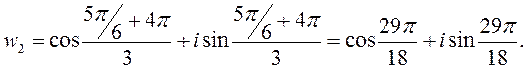
Рекомендуемая литература

ОСНОВНАЯ ЛИТЕРАТУРА

№	Наименование учебников и учебных пособий	Кол-во экз. в библ.
1.	Математика. Методические указания и контрольные задания для студентов – заочников инженерно – технических специальностей/ сост.:Г.А. Циценкова, Т.В. Чукавина, Л.Д.Рязанова, В.А. Труппова- Иркутск: Изд-во ИрГТУ,2006. – 112с.
1.	Письменный Дмитрий Трофимович, Конспект лекций по высшей математике: Полный курс / Дмитрий Письменный.- 6-е изд.,. - М.: Айрис-пресс, 2007. - 602 с.
2.	Письменный Дмитрий Трофимович. Конспект лекций по высшей математике: в 2 ч. / Дмитрий Письменный - Ч.1.- Тридцать шесть лекций. - Изд. 5-е, 2005. - 279 с.
3.	Письменный Дмитрий Трофимович. Конспект лекций по высшей математике: в 2 ч. / Д. Т. Письменный Ч. 2. - Тридцать пять лекций. - Изд. 2-е, 2005. - 251 с.
4.	Данко П.Е., Попов А.Г., Кожевникова Т.Я. Данко С.П. Высшая математика в упражнениях и задачах В 2 ч. Ч.2. Учебное пособие для вузов – М: ООО «Издательство Оникс»: ООО «Издательство Мир и Образование», 2007.- 416 с.

ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА

№	Наименование учебников и учебных пособий	Кол-во экз. в библ.
1.	Сборник задач по высшей математике: С контрол. работами. 1 курс / К. Н. Лунгу [и др.]. - Изд. 3-е, испр. и доп. - М.: Айрис-пресс, 2004.
2.	Сборник задач по высшей математике: С контрол. работами. 2 курс / К. Н. Лунгу [и др.]. - Изд. 3-е, испр. и доп. - М.: Айрис-пресс, 2004.
3.	Потёмкина С.П. Математика. Методическое пособие для студентов инженерно-технических специальностей заочной формы обучения-2005г