Многогранник – это замкнутая пространственная фигура, ограниченная плоскими многоугольниками (частями пересекающихся плоскостей).
Выпуклые многоугольники – это такие многоугольники, у которых все вершины и ребра находятся по одну сторону любой из их граней.
Наибольший интерес представляют призмы, пирамиды и правильные выпуклые многоугольники – тела Платона.
Призма – это многогранник, две грани которого представляют собой равные многоугольники (основания призмы) со взаимно параллельными сторонами, все другие грани – параллелограммы (или прямоугольники).
Пирамида – это многогранник, одна грань которого – многоугольник, а остальные грани – треугольники с общей вершиной.
Тела Платона – это многогранники, все грани которых представляют собой правильные и равные многоугольники. Углы при вершинах таких многоугольников равны между собой. Существует 5 типов правильных многогранников: гексаэдр (куб) – 6 квадратов; тетраэдр; октаэдр; икосаэдр – 4, 8 и 20 правильных треугольников; додекаэдр – 12 правильных пятиугольников.
6.1.2. Некоторые позиционные задачи на пересечение
многогранника с прямой и плоскостью
Плоскость пересекает многогранную поверхность по плоской замкнутой ломаной линии, называемой фигурой сечения. Вершины и стороны фигуры сечения определяются пересечением заданной плоскости соответственно с рёбрами и гранями многоугольника. То есть многократно решается задача или на пересечение двух плоскостей (граней многогранника с секущей плоскостью), или на пересечение прямой с плоскостью (рёбер многогранника с секущей плоскостью). Это уже известные задачи.
Пример 1.Дана треугольная наклонная пирамида и секущая фронтально проецирующая плоскость å (рис. 6.1). Определить проекции фигуры сечения.
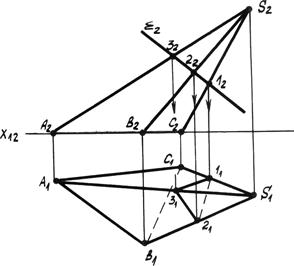
Рис. 6.1
Решение.Так как секущая плоскость является фронтально проецирующей, то фронтальная проекция фигуры сечения (12 22 32) совпадет со следом плоскости å 2. Фигура сечения является треугольником и определяется на пересечении следа плоскости с соответствующими ребрами пирамиды. По линиям связи определяются горизонтальные проекции вершин треугольника (11 21 31) на соответствующих ребрах пирамиды. Далее определяется видимость звеньев линии сечения в зависимости от видимости граней пирамиды на горизонтальной проекции.
Пример 2.Дана прямая треугольная призма и секущая плоскость общего положения Т (рис. 6.2). Определить проекции фигуры сечения.
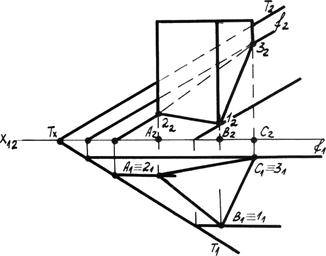
Рис. 6.2. Пересечение многогранника плоскостью
Решение. Так как боковые грани призмы являются горизонтально проецирующими плоскостями, то горизонтальная проекция фигуры сечения совпадает с горизонтальной проекцией призмы, т.е. (А 1 В 1 С 1) º (112131). Решение задачи сводится к определению второй проекции точек сечения, принадлежащих и плоскости Т и призме.
Для этого воспользуемся фронталями плоскости ¦, проведенными через соответствующие точки 11 º В 1, 21 º А 1, 31 º С 1. Фронтальную проекцию фигуры сечения (12 22 32) определяем на пересечении фронтальных проекций фронталей с соответствующими рёбрами призмы.
Определяем видимость звеньев линии сечения.
Пример 3. Дана прямоугольная пирамида и секущая плоскость общего положения Т (рис. 6.3). Определить проекции фигуры сечения.
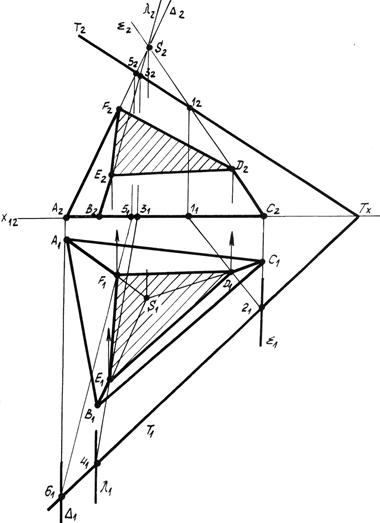 |
Рис. 6.3
Решение. Ребра и грани пирамиды являются геометрическими объектами общего положения. Определим точки фигуры пересечения, решая несколько раз задачу на пересечение прямой с плоскостью (ребрá пирамиды с секущей плоскостью). Для этого заключаем последовательно каждое ребро во вспомогательную фронтально проецирующую плоскость: ребро АS – в плоскость D (D2 º А 2 S 2), ребро ВS – в плоскость l (l2 º В 2 S 2), ребро СS – в плоскость å (å2 º С 2 S 2). Определяем линию пересечения каждой вспомогательной плоскости с секущей плоскостью – линии (1121), (3141), (5161). На пересечении линий пересечения и проекций соответствующих ребер определяем искомые точки фигуры сечения (D 1 E 1 F 1), (D 2 E 2 F 2).
Пример 4. Дана прямоугольная пирамида и прямая общего положения l (рис. 6.4). Определить точки пересечения прямой и пирамиды.
Решение. Так как прямая l является прямой общего положения, задача решается аналогично задаче нахождение точки пересечения прямой и плоскости. Заключаем прямую l во вспомогательную фронтально проецирующую плоскость å (å2 º l 2). Строим сечение пирамиды вспомогательной плоскостью å (аналогично задаче 1, рис. 6.1). На пересечении горизонтальной проекции прямой l 1 c контуром сечения (112131) находим искомые точки D и E. Определяем видимость прямой относительно точек пересечения с пирамидой.
 2015-04-12
2015-04-12 3362
3362








