2015-04-12
3358
Линейчатыми называются поверхности, образованные движением прямой линии по определенному закону.
Развертывающимися (торсовыми) называются поверхности, которые можно развернуть на плоскости без складок и разрывов. К развертывающимся линейчатым поверхностям относятся: цилиндрическая; призматическая; коническая; пирамидальная. Данные линейчатые поверхности имеют одну направляющую.
1. Цилиндрическая поверхность Г (n, s) (Рис.19)
(n, s) –определитель поверхности. Состав определителя: n – направляющая (кривая линия);
s – направление образующей (образующая – прямая линия).
Закон образования поверхности (закон Каркаса): l i x n; l i II s.
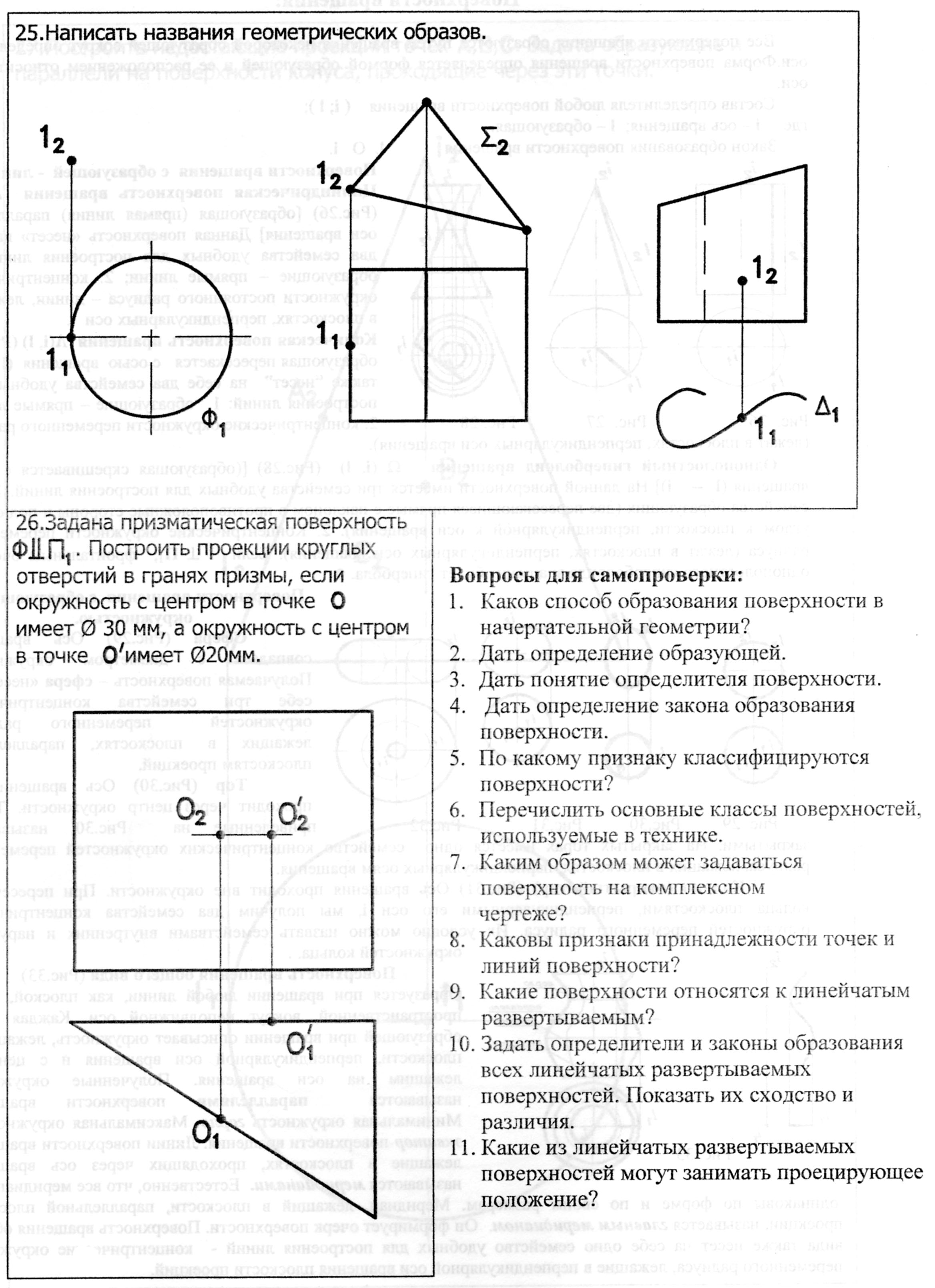
2. Призматическая поверхность L (n, s) (Рис.20)
(n, s)–определитель поверхности. Состав определителя: n – направляющая (ломаная линия);
s – направление образующей (образующая – прямая линия).
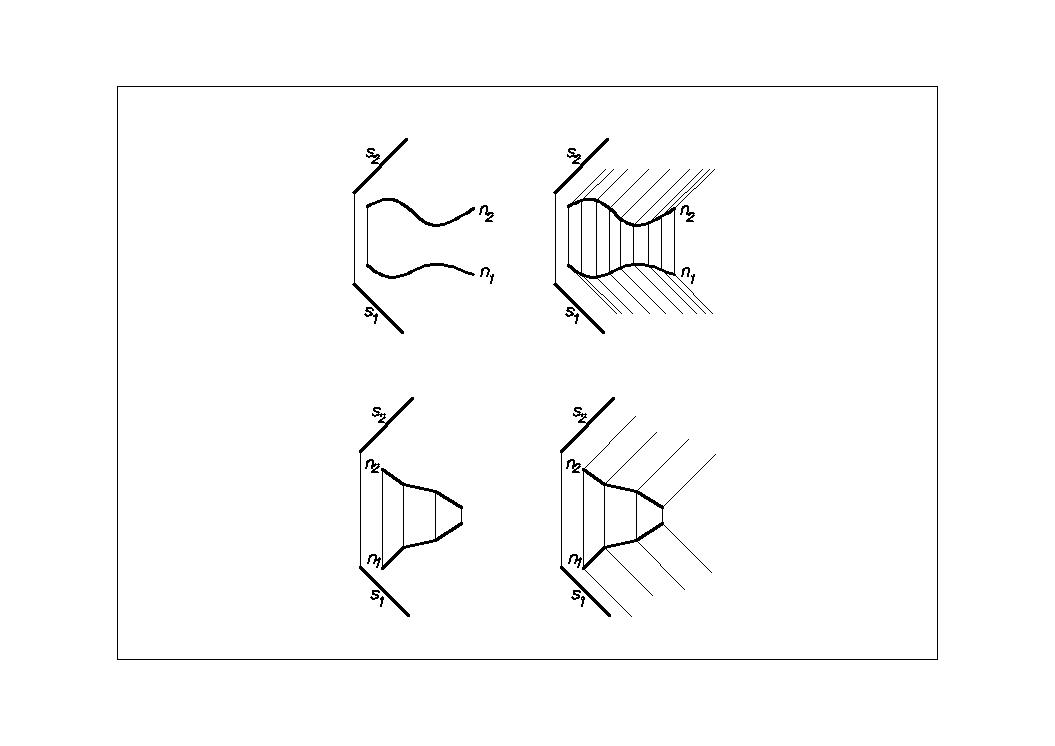Закон образования поверхности (закон Каркаса): l i x n; l i II s.
Рис.19 Рис.20
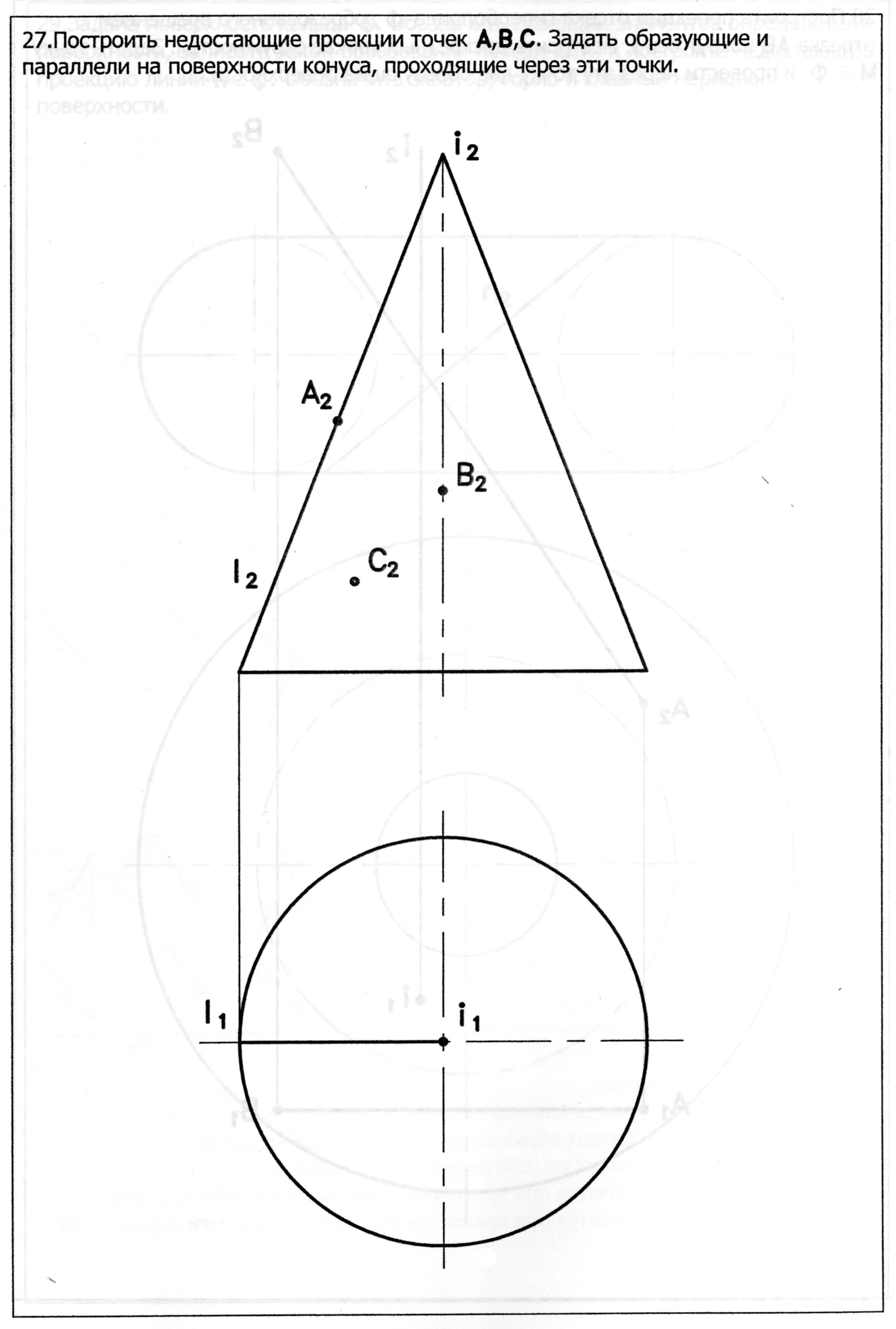
3. Коническая поверхность D (n, S) (Рис.21)
(n, S) –определитель поверхности. Состав определителя: n – направляющая (кривая линия);
S – вершина поверхности.
Закон образования поверхности: l i x n; l i Ì s.
4. Пирамидальная поверхность V (n,S) (Рис.22)
(n, S) –определитель поверхности. Состав определителя: n – направляющая (ломаная линия);
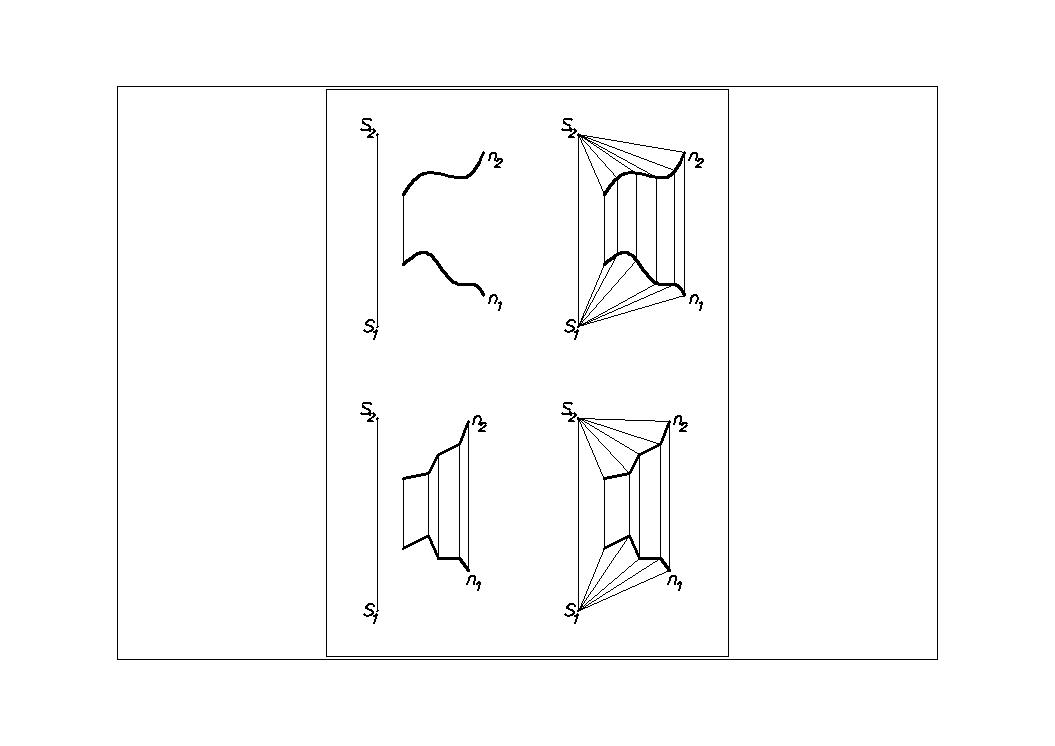S – вершина поверхности;
Закон образования поверхности: l i x n; l i Ì S.
Рис.21 Рис.22
1. Каков способ образования поверхности в начертательной геометрии?
2. Дать определение образующей.
3. Дать понятие определителя поверхности.
4. Дать определение закона образования поверхности.
5. По какому признаку классифицируются поверхности?
6. Перечислить основные классы поверхностей, используемых в технике.
7. Каким образом может задаваться поверхность на комплексном чертеже?
8. Каковы признаки принадлежности точек и линий поверхности?
9. Какие поверхности относятся к линейчатым поверхностям?
10. Задать определители и законы образования всех линейчатых развертываемых поверхностей. Показать их сходство и различие.
11. Какие из линейчатых развертываемых поверхностей могут занимать проецирующее положение?
Все поверхности вращения образуются путем вращения некоторой образующей вокруг определенной оси. Форма поверхности вращения определяется формой образующей и ее расположением относительно оси.
Состав определителя любой поверхноcти вращения (i; l);
где i – ось вращения; l – образующая.
Закон образования поверхности вращения l Ο i.
Поверхности вращения с образующей - линией.
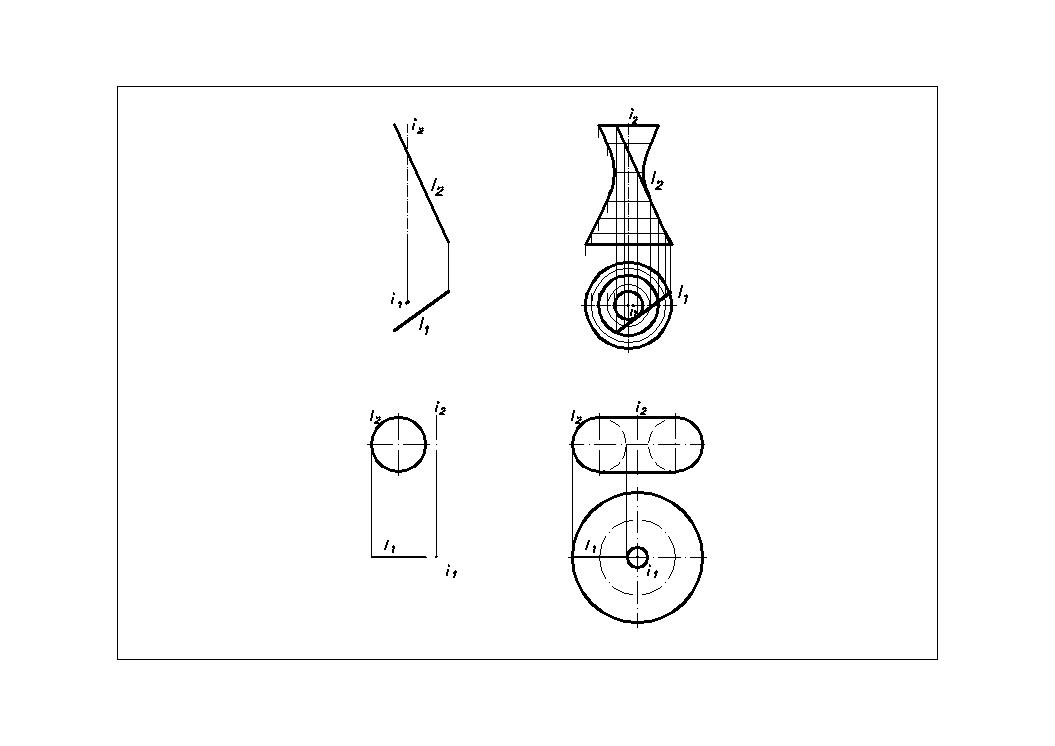
Цилиндрическая поверхность вращения D (i, l) (Рис.26) [образующая (прямая линия) параллельна оси вращения] Данная поверхность «несет» на себе два семейства удобных для построения линий: 1. образующие – прямые линии; 2. концентрические окружности постоянного радиуса – линии, лежащие в плоскостях, перпендикулярных оси i.
Коническая поверхность вращения L (i, l) (Рис.27) образующая пересекается с осью вращения (l х i ]
также “несет” на себе два семейства удобных для построения линий: 1. образующие – прямые линии; Рис. 26 Рис. 27 Рис. 28 2. концентрические окружности переменного радиуса (лежат в плоскостях, перпендикулярных оси вращения).
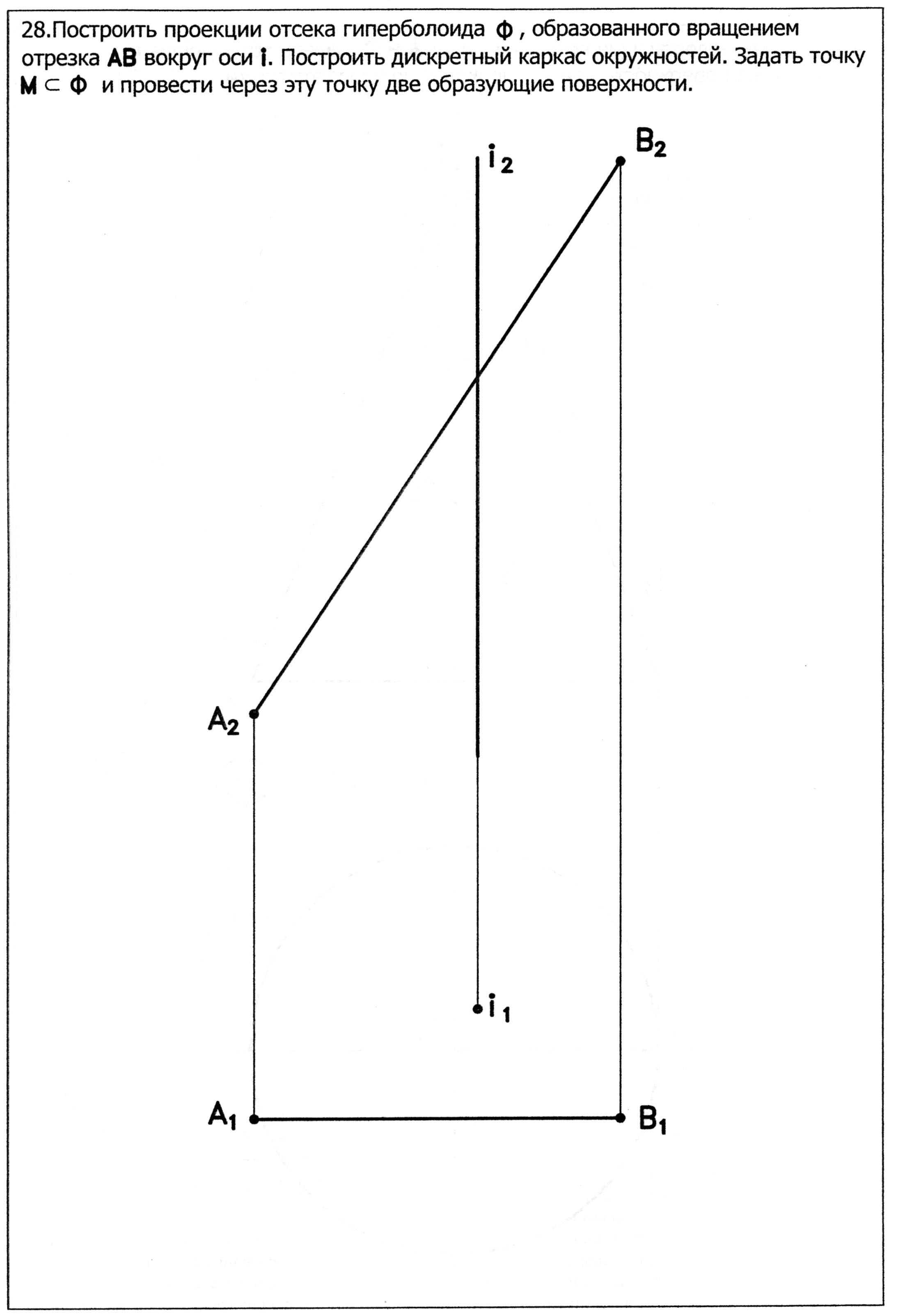
Однополостный гиперболоид вращения W (i, l) (Рис.28) [(образующая скрещивается с осью вращения (l -- i)] На данной поверхности имеется три семейства удобных для построения линий. 1. Два семейства образующих (две пересекающиеся прямые с наклоном в противоположные стороны и под одним углом к плоскости, перпендикулярной к оси вращения). 2. Концентрические окружности переменного радиуса (лежат в плоскостях, перпендикулярных оси вращения). Если I ^ П 1, фронтальным очерком однополостного гиперболоида вращения будет гипербола.
Поверхности вращения с образующей - окружностью.
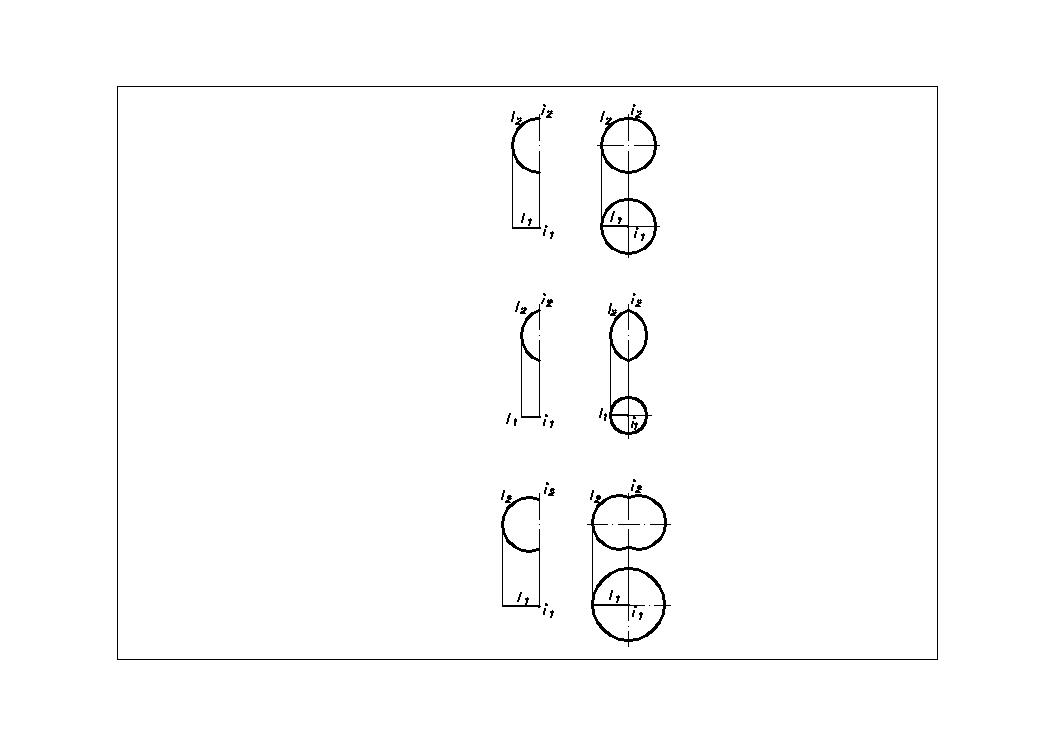
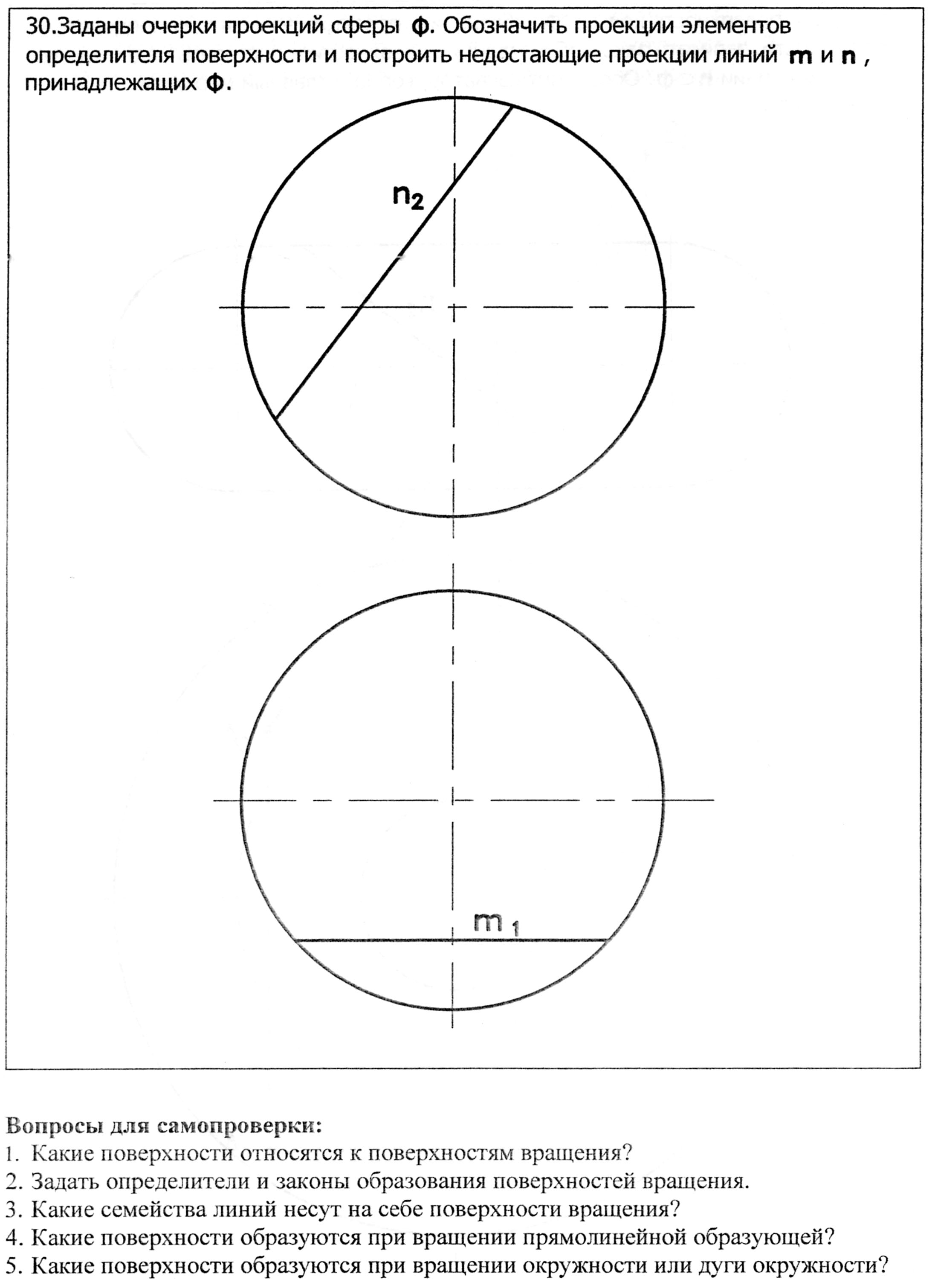
Сфера (Рис.29) Ось вращения совпадает с диаметром окружности. Получаемая поверхность – сфера «несет» на себе три семейства концентрических окружностей переменного радиуса. лежащих в плоскостях, параллельных плоскостям проекций.
Тор (Рис.30) Ось вращения не проходит через центр окружности. Торы, Рис. 29 Рис.30 Рис.31 Рис.32 приведенные на Рис.30, называются закрытыми. На закрытых торах имеется одно семейство концентрических окружностей переменного радиуса, лежащих в плоскостях, перпендикулярных осям вращения.
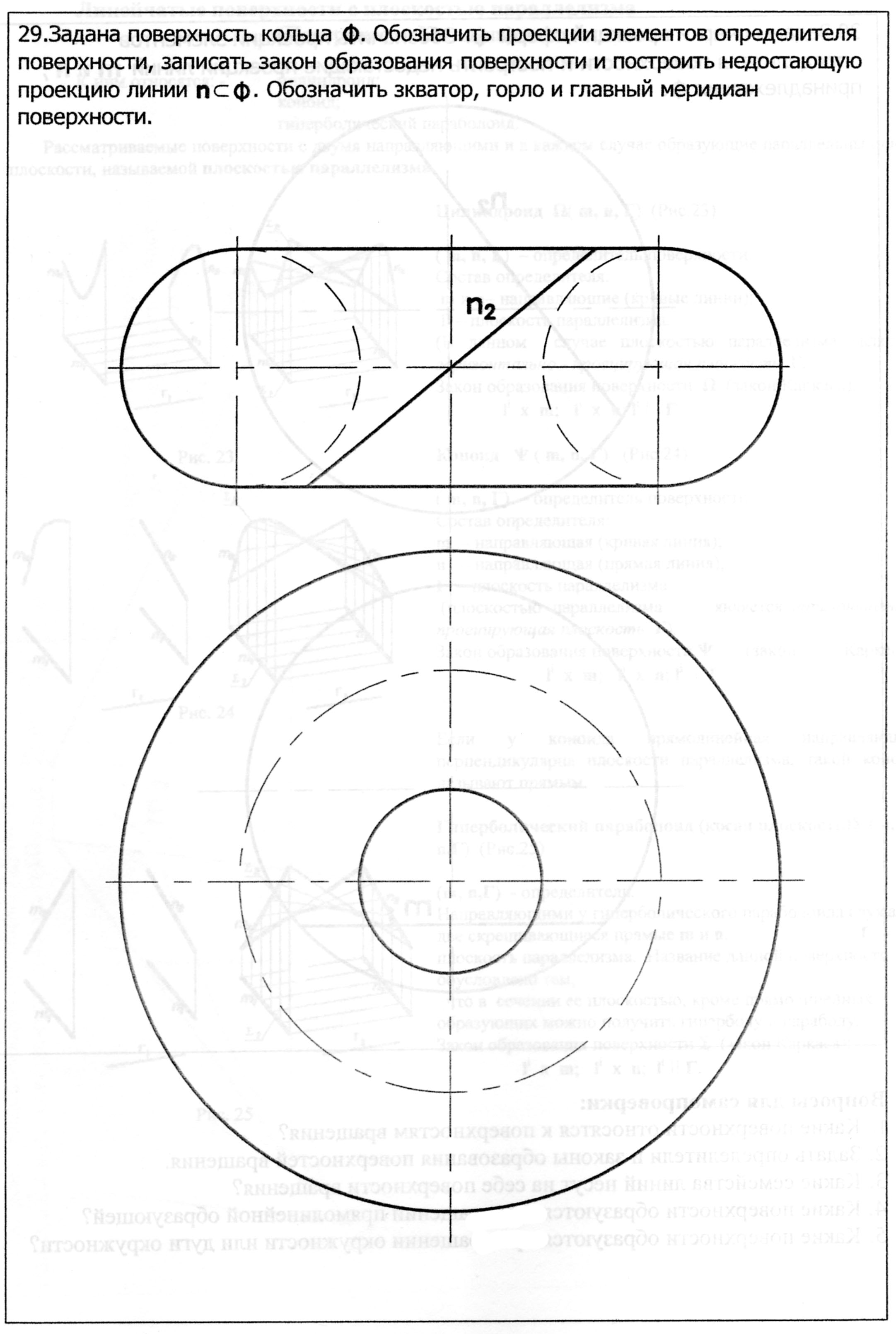
Кольцо (открытый тор) (Рис.31) Ось вращения проходит вне окружности. При пересечении кольца плоскостями, перпендикулярными его оси i, мы получим два семейства концентрических окружностей переменного радиуса. Их условно можно назвать семействами внутренних и наружных окружностей кольца..
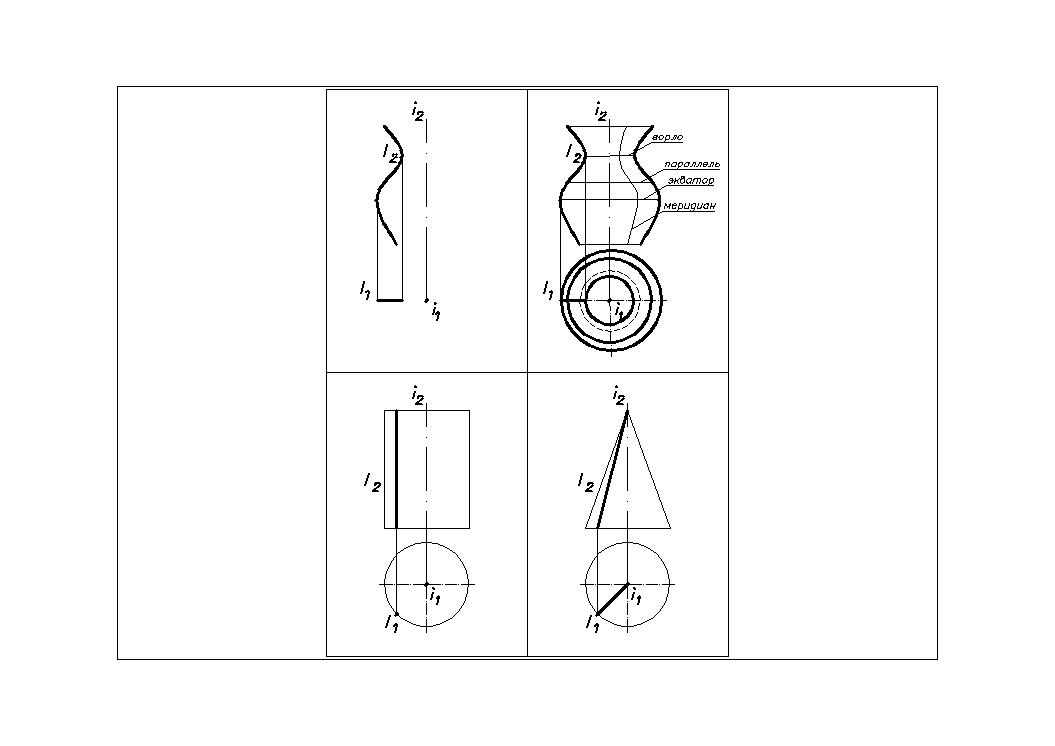
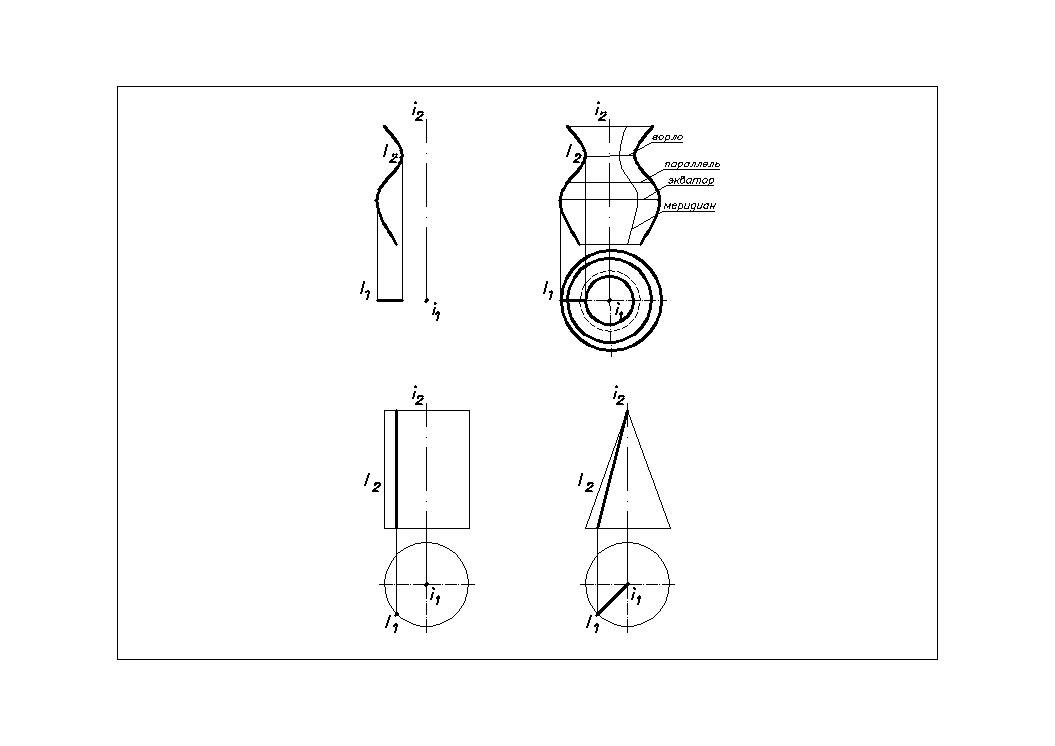Поверхность вращения общего вида (Рис.33)
Образуется при вращении любой линии, как плоской, так и пространственной, вокруг неподвижной оси. Каждая точка образующей при вращении описывает окружность, лежащую в плоскости, перпендикулярной оси вращения и с центром, лежащим на оси вращения. Полученные окружности называются параллелями поверхности вращения. Минимальная окружность горло. Максимальная окружность – экватор поверхности
| Рис. 33 |
вращения. Линии поверхности вращения, лежащие в плоскостях, проходящих через ось вращения, называются меридианами. Естественно, что все меридианы
одинаковы по форме и по своим размерам. Меридиан, лежащий в плоскости, параллельной плоскости проекции, называется главным меридианом. Он формирует очерк поверхности. Поверхность вращения общего вида также несет на себе одно семейство удобных для построения линий - концентрические окружности переменного радиуса, лежащие в перпендикулярной оси вращения плоскости проекций.
