Общее уравнение кривых второго порядка имеет вид
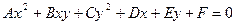 , (1)
, (1)
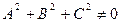 .
.
График уравнения (1) определяется его инвариантом 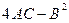 , неизменным при параллельном переносе и повороте осей координат:
, неизменным при параллельном переносе и повороте осей координат:
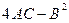 >0 – эллипс (окружность),
>0 – эллипс (окружность),
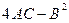 =0 – парабола,
=0 – парабола,
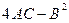 <0 – гипербола.
<0 – гипербола.
Окружность – множество всех точек плоскости, равноудаленных от заданной точки, называемой центром (рис. 13).
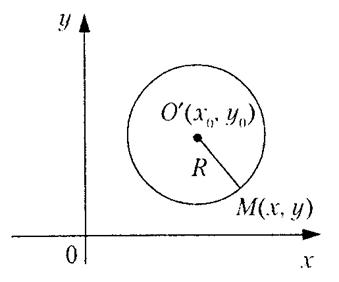
Рис. 13.
Нормальные уравнения окружности радиуса R с центром в точках 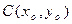 и О(0,0) соответственно
и О(0,0) соответственно
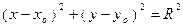 , (2)
, (2)
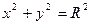 .
.
Пример. Найти координаты центра и радиус окружности
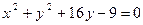 .
.
Решение. Уравнение представлено в общем виде (1). Запишем его в виде (2)
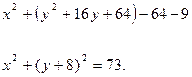
Таким образом, центр окружности в точке О(0,-8), а радиус 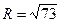 .
.
Эллипс – множество всех точек плоскости, для каждой из которых сумма расстояний до двух заданных фиксированных точек, называемых фокусами (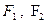 ), есть величина постоянная (рис. 14).
), есть величина постоянная (рис. 14).
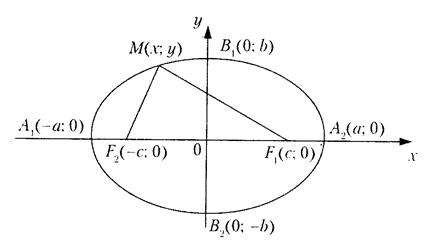
Рис. 14.
Каноническое уравнение эллипса (координатные оси совпадают с осями эллипса)
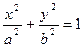 .
.
Некоторые обозначения и характеристики эллипса:
a, b – полуоси эллипса,
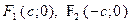 – фокусы эллипса, если a>b (
– фокусы эллипса, если a>b ( 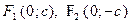 , если a<b),
, если a<b),
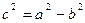 (a>b), (
(a>b), (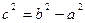 (a<b)),
(a<b)),
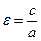 <1 – эксцентриситет эллипса,
<1 – эксцентриситет эллипса,
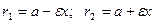 – расстояния от точки M(x,y) эллипса до его фокусов (фокальные радиусы).
– расстояния от точки M(x,y) эллипса до его фокусов (фокальные радиусы).
Пример. Определить вид и расположение кривой
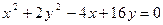 .
.
Решения. Так как 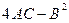 =4*1*2-0>0, то уравнение эллиптического типа.
=4*1*2-0>0, то уравнение эллиптического типа.
Приведем уравнение к каноническому виду, выделяя полные квадраты,
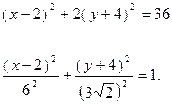
Следовательно, кривая представляет собой эллипс с полуосями 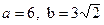 , центр которого находится в точке O’(2;-4) (рис. 15).
, центр которого находится в точке O’(2;-4) (рис. 15).
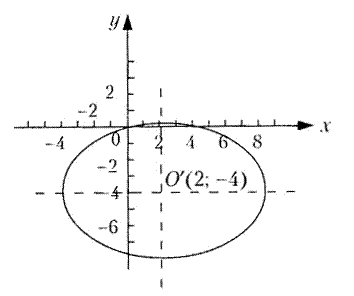
Рис. 15.
Гипербола – это множество всех точек плоскости, для каждой из которых модуль разности расстояний до двух заданных фиксированных точек, называемых фокусами, есть величина постоянная (рис.16).
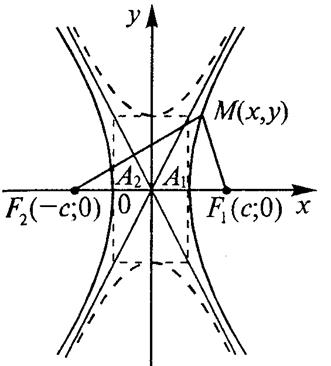
Рис. 16.
Каноническое уравнение гиперболы (координатные оси совпадают с осями гиперболы)
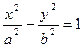 , фокусы на ОХ;
, фокусы на ОХ;
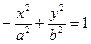 , фокусы на ОY.
, фокусы на ОY.
Некоторые обозначения и характеристики гиперболы:
a, b – соответственно действительная и мнимая полуоси гиперболы (наоборот, мнимая и действительная, для гиперболы 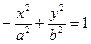 );
);
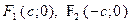 – фокусы гиперболы (
– фокусы гиперболы (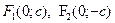 для гиперболы
для гиперболы 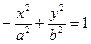 );
);
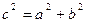 ,
,
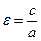 >1 – эксцентриситет гиперболы,
>1 – эксцентриситет гиперболы,
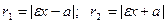 – расстояния от точки M(x,y) эллипса до его фокусов (фокальные радиусы),
– расстояния от точки M(x,y) эллипса до его фокусов (фокальные радиусы),
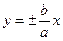 – уравнение обеих асимптот гиперболы;
– уравнение обеих асимптот гиперболы;
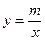 – обратная пропорциональная зависимость.
– обратная пропорциональная зависимость.
Пример. Написать уравнение гиперболы с асимптотами 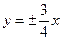 , проходящей через точку
, проходящей через точку 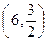 . Найти расстояние между ее вершинами.
. Найти расстояние между ее вершинами.
Решение. 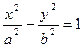 .
.
Полуоси гиперболы найдем из системы
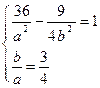
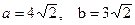 .
.
Расстояние между вершинами равно 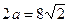 (рис. 17).
(рис. 17).
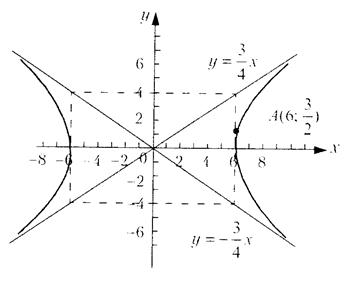
Рис. 17.
Парабола – множество всех точек плоскости, равноудаленных от заданной точки, называемой фокусом, и заданной прямой, называемой директрисой (рис. 18).

Рис. 18.
Каноническое уравнение параболы с вершиной в начале координат
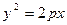 ,
,
если она симметрична относительно оси Ох,
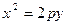 ,
,
если она симметрична относительно оси Оy.
Некоторые обозначения и характеристики параболы:
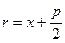 – расстояние от произвольной точки M (x,y) параболы до фокуса
– расстояние от произвольной точки M (x,y) параболы до фокуса 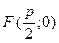 параболы (фокальный радиус), расстояние от произвольной точки M (x,y) параболы до директрисы,
параболы (фокальный радиус), расстояние от произвольной точки M (x,y) параболы до директрисы,
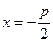 – уравнение директрисы параболы.
– уравнение директрисы параболы.
Пример 1. Построить кривую 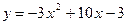 .
.
Решение. 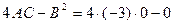 =0 – парабола.
=0 – парабола.
Выделим полные квадраты:
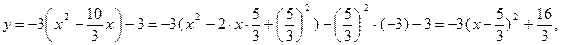
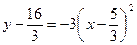 .
.
Пусть 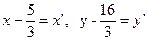 ,
,
Тогда получим
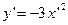 или
или 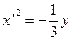 .
.
Таким образом, парабола имеет вершину 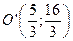 и ось симметрии
и ось симметрии 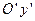 , параллельную оси Oy (рис. 19).
, параллельную оси Oy (рис. 19).
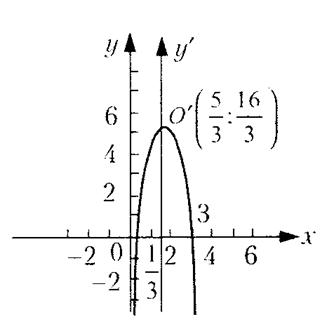
Рис. 19.
Пример 2. Из контрольной работы, вариант 5, задание 5.
 2015-04-12
2015-04-12 1385
1385

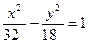 .
.