2015-04-12
1877
1. Алгоритм Квайна. Напомним, что формула F от пропозициональных переменных А1, А2, …, Аn является общезначимой (тождественно истинной) или (что то же самой) доказуемой, если булева функция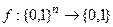 
, соответствующая формуле F, тождественно равна 1. Для проверки значений функции f используется так называемое семантическое дерево, т.е. бинарное дерево, которое удовлетворяется следующим условиям:
1) каждое ребро соответствует переменной (с отрицанием или без);
2) ребра, выходящие из одной вершины, соответствуют контрарным переменным: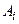 
, 
;
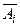3) ребра соответствуют одной и той же переменной 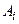тогда и только тогда, когда они находятся на одинаковом расстоянии от корня (рис. 1.1).
 |
Семантическое дерево имеет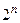 
висячих вершин и для проверки общезначимости необходимо пройти 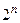маршрутов от корня до этих вершин.
Алгоритм Квайна позволяет проходить не все семантическое дерево, а только его часть. Он состоит в том, что пропозициональным переменным 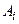, упорядоченным в набор (А1, А2, …, Аn), последовательно придают значения 0 и 1 и анализируют таблицы истинности формул, содержащих меньшее число переменных.
Пример. Проверить общезначимость формулы
.
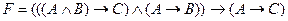Упорядочим пропозициональные переменные (А, В, С). Придадим первой переменной А значение 1, т.е. А =1. Тогда формула F преобразуется следующим образом:
.
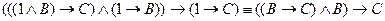В полученной формуле переменной В придадим значение 1, т.е. В =1. Тогда преобразованная формула имеет вид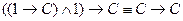 
, т.е. будет общезначимой. В случае В =0 имеем 
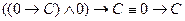, что также общезначимо. Рассмотрим теперь случай А =0. Имеем
.
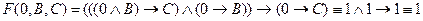Таким образом, все возможные случаи приводят к тождественно истинным (общезначимым) формулам. Следовательно, формула F также истинна. На рис. 1.2а изображено семантическое дерево, соответствующее формуле F, а на рис. 1.2б показана часть семантического дерева, которая фактически использовалась для проверки общезначимости.
 |
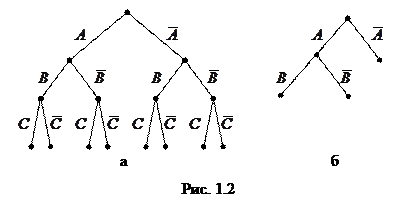2. Алгоритм редукции решает ту же задачу проверки общезначимости формулы, но используется в том случае, когда в формуле содержится достаточно много импликаций. Идея алгоритма состоит в попытке нахождения значений пропозициональных переменных формулы F, при которых значение функции f равно 0, на основе того, что импликация является ложной в том и только в том случае, когда посылка истинна, а заключение ложно.
Пример. Проверить тождественную истинность формулы
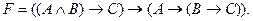
Предположим, что формула ложна при некотором наборе значений переменных А, В, С. Тогда истинностная функция f по этим значениям переменных дает следующие значения формул: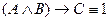 
, 
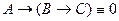. Тогда из второго равенства получает А =1, 
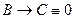, откуда имеем B =1, C =0. Однако при этих значениях справедливо 
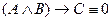. Получили противоречие. Таким образом, формула F тождественно истинна.
