Для алгебры высказываний существует в известном смысле адекватная аксиоматическая логическая система, которая называется исчислением высказываний.
Введем понятие формального исчисления. Будем говорить, что формальное исчисление I определено, если выполняются следующие четыре условия:
1. Имеется некоторое множество А символов – алфавит исчислния I. Конечные последовательности символов называют словами или выражениями исчисления I. Обозначим через S множество всех слов алфавита исчисления I.
2. Задано подмножество F Í S, называемое множеством формул исчислния I. Элементы множества F называют формулами.
3. Выделено подмножество формул H Í F, называемых аксиомами исчисления I.
4. Имеется конечное множество R отношений 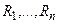 между формулами, называемых правилами вывода.
между формулами, называемых правилами вывода.
Если 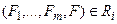 , то
, то 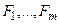 называются посылками, а F называется непосредственным следствием формул
называются посылками, а F называется непосредственным следствием формул 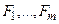 по правилу
по правилу 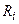 или заключением правила
или заключением правила 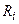 .
.
Итак, исчисление I есть четверка (A, F, H, R).
Выводом в исчислении называется последовательность формул 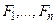 такая, что для любого i
такая, что для любого i 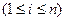 формула Fi есть либо аксиома исчисления, либо непосредственное следствие каких-либо предыдущих формул.
формула Fi есть либо аксиома исчисления, либо непосредственное следствие каких-либо предыдущих формул.
Формула F называется теоремой исчисления, выводимой в исчислении или доказуемой в исчислении, если существует вывод 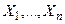 , F, который называют выводом формулы F или доказательством теоремы F.
, F, который называют выводом формулы F или доказательством теоремы F.
Вообще говоря, может не существовать алгоритма, с помощью которого для произвольной формулы через конечное число шагов можно определить, является ли она выводимой в исчислении или нет. Если такой алгоритм существует, то исчисление называется разрешимым, иначе неразрешимыми.
Используя понятие формального исчисления, определим исчисление высказываний.
Символами исчисления высказываний являются во-первых, заглавные латинские буквы, с индексами или без, которыми обозначаются высказывания, во-вторых, знаки логических операций и, в-третьих, пара скобок (). Иных символов, кроме указанных, исчисление высказываний не имеет.
Формулы исчисления высказываний представляют собой конечные последовательности описанных символов. Эти последовательности, как правило, записываются в виде строчек. Не всякая строка символов является формулой. Полное определение формулы имеет рекурсивный характер: указываются некоторые исходные формулы и затем правила, позволяющие из формул образовывать новые формулы. Таким образом, определение формулы можно сформулировать следующим образом:
1. Все пропозициональные переменные являются формулами исчисления высказываний (элементарные формулы).
2. Если X и Y – формулы исчисления высказываний, то 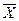 , X Ù Y, X Ú Y, X ® Y также формулы исчисления высказываний.
, X Ù Y, X Ú Y, X ® Y также формулы исчисления высказываний.
3. Выражение является формулой исчисления высказываний тогда и только тогдая, когда это может быть установлено с помощью пунктов 1 и 2.
Таким образом, любая формула исчисления высказываний строится из пропозоциональных переменных с помощью логических операций  , Ù, Ú, ®.
, Ù, Ú, ®.
Для доказательства того, что некоторая последовательность символов является формулой, необходимо показать, что она удовлетворяет определению формулы, т. е. требуется произвести ее конструкцию по указанной в определении схеме, так что при построении формулы мы должны построить и все ее части, называемые подформулами.
Пример.Чтобы доказать, что последовательность ((X Ù Y) ® (X Ú Z)) является формулой, мы должны рассуждать следующим образом: так как X и Y формулы, то (X Ù Y) – также формула, так как X и Z – формулы, то (X Ú Z) – также формула; так как (X Ù Y) и (X Ú Z) – формулы, то
((X Ù Y) ® (X Ú Z)) – также формула.
Следующим шагом в определении исчисления высказываний является определение некоторого класса формул, которые называются истинными или выводимыми в исчислении высказываний. Определение истинных формул имеет такой же рекурсивный характер, как и определение формулы. Сначала определяются исходные истинные формулы, а затем определяются правила, позволяющие из имеющихся истинных формул образовывать новые. Эти правила называются правилами вывода, а исходные истинные формулы – аксиомами. Образование истинной формулы из исходных истинных формул или аксиом путем применения правил вывода называется выводом данной формулы из аксиом.
Для полного набора логических связок: импликация, отрицание, конъюнкция и дизъюнкция система содержит десять аксиом. В силу полноты систем, использующих логические связки а) импликации и отрицания, б) импликации и дизъюнкции, в) импликации, отрицания, конъюнкции и дизъюнкции можно использовать в процессе дедуктивного вывода любую из указанных систем.
Ниже приведена одна из систем аксиом:
1. ├─ X ®(Y ® X);
2. ├─(X ® Y)®((X ®(Y ® Z))®(X ® Z));
3. ├─ X Ù Y ® X;
4. ├─ X Ù Y ® Y;
5. ├─(X ® Y)®((X ® Z)®(X ® Y Ù Z));
6. ├─ X ® X Ú Y;
7. ├─ Y ® X Ú Y;
8. ├─(X ® Z)®((Y ® Z)®(X Ú Y ® Z));
9. ├─(X ® Y)®((X ® 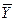 )®
)® 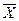 );
);
10. ├─ 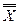 ® X;
® X;
К правилам вывода в исчислении высказываний относятся следующие:
1. Правило подстановки.
Если выводимая формула F содержит некоторую переменную Х (обозначим этот факт F (Х)) и существует произвольная формула B, то формула F (B), получающаяся заменой всех вхождений Х на формулу B, также выводима в исчислении высказываний. Этот факт формально описывают так:
Этот факт записывают так: 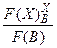 .
.
Если F (A)= A, то 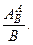 Если
Если 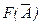 , то
, то 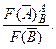
Следует еще раз обратить внимание, что формула F должна быть выводимой в исчислении высказываний.
Пример. Пусть даны формулы F = A ®(C ® A)и B = C ® 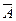 .
.
Если выполнить подстановку формулы B в формулу F вместо формулы A, то получим новую формулу F `.
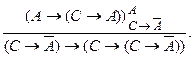
2. Правило заключения (modus ponens).
Если А и А ® В – истинные формулы в исчислении высказываний, то В также истинная формула.
Пример. Если формулы истинны 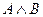 и
и 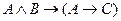 , то формула
, то формула 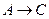 тоже истинна.
тоже истинна.
Указанием аксиом и правил вывода мы полностью определяем понятие истинной или выводимой в исчислении высказываний формулы. Пользуясь правилами вывода, мы можем исходя из аксиом, конструировать новые истинные формулы и получать таким образом каждую истинную формулу. Кроме основных правил вывода – правила подстановки и правила заключения, существуют и другие правила образования истинных формул, производные от основных правил и являющиеся сокращением многократного применения основных правил. Правила выражаются обычно в следующих терминах: «если формулы А, В,... истинны, то формулы Х, Y,... также истинны» и записываются в виде 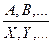 .
.
Наряду с правилом modus ponens, используют следующее правило. Если 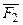 и
и 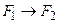 – истинные формулы в исчислении высказываний, то
– истинные формулы в исчислении высказываний, то 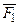 также истинная формула. Это правило modus tollens (m. t.).
также истинная формула. Это правило modus tollens (m. t.).
Утверждение, что формула F выводима из формул F 1, F 2,..., Fn записывается в виде F 1, F 2,..., Fn ├─ F.
Говорят, что формула F выводима из формул F 1, F 2,..., Fn, если существует последовательность формул F 1, F 2,..., Fk, F, в которой любая формула либо является аксиомой, либо принадлежит списку формул F 1, F 2,..., Fn, называемых гипотезами, либо получается из предыдущих по правилам вывода.
Расширим понимание выражения F 1, F 2,..., Fn ├─ F на случай, когда формулы F 1, F 2,..., Fn отсутствуют, считая, что тогда F является просто истинной формулой исчисления высказываний. Этот факт обозначается в виде ├─ F и равносилен тому, что F – теорема исчисления высказываний.
Пример. Покажем, что формула 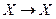 выводима в исчислении высказываний. Для этого построим вывод данной формулы:
выводима в исчислении высказываний. Для этого построим вывод данной формулы:
1) в схеме аксиом 2 Y заменим на 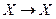 , Z – на X. Получим
, Z – на X. Получим 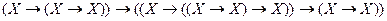 ;
;
2) в схеме аксиом 1 Y заменим на X. Получим 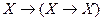 ;
;
3) из 1 и 2 по правилу заключения получим
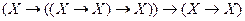 ;
;
4) в схеме аксиом 1 заменим Y на 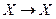 , получим
, получим
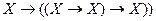 ;
;
5) из 3 и 4 по правилу заключения справедливо ├─ 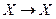 .
.
Для того чтобы установить выводимость различных формул более простым путем, чем непосредственный вывод этих формул, используется так называемая теорема дедукции.
Теорема о дедукции. Если 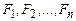 , F ├─ B, то
, F ├─ B, то 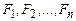 ├─ F ® B.
├─ F ® B.
Утверждение 1. Тогда и только тогда 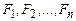 ├─ F, когда
├─ F, когда 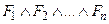 ├─ F (сведение множества посылок к одной посылке).
├─ F (сведение множества посылок к одной посылке).
Утверждение 2. Если 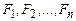 , F, В - формулы исчисления высказываний,
, F, В - формулы исчисления высказываний, 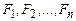 ├─ B, то
├─ B, то 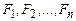 , F ├─ B (можно увеличить число посылок).
, F ├─ B (можно увеличить число посылок).
Следствие из теоремы о дедукции. Тогда и только тогда F выводима из формул 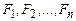 , когда ├─ F 1 ®(F 2 ® (...(Fn ® F)...)).
, когда ├─ F 1 ®(F 2 ® (...(Fn ® F)...)).
Доказательство. Пусть 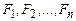 ├─ F, тогдана основании утверждения 1
├─ F, тогдана основании утверждения 1 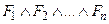 ├─ F. Применив теорему о дедукции, получим ├─
├─ F. Применив теорему о дедукции, получим ├─ 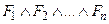 ® F. Используя правила эквивалентных преобразований алгебры высказываний, получим
® F. Используя правила эквивалентных преобразований алгебры высказываний, получим
1) ├─ (F 1Ù F 2Ù...Ù Fn ® F);
2) ├─ (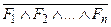 Ú F);
Ú F);
3) ├─ (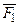 Ú
Ú 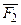 Ú...Ú
Ú...Ú 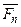 Ú F);
Ú F);
4) ├─ (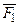 Ú
Ú 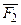 Ú...Ú
Ú...Ú 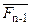 Ú(Fn ® F));
Ú(Fn ® F));
5) ├─ (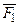 Ú
Ú 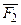 Ú...Ú(Fn-1 ®(Fn ® F)));
Ú...Ú(Fn-1 ®(Fn ® F)));
6) ├─ (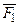 Ú (F2 ®...®(Fn-1 ®(Fn ® F))...));
Ú (F2 ®...®(Fn-1 ®(Fn ® F))...));
7) ├─ (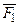 ®(F2 ®...®(Fn-1 ®(Fn ® F))...).
®(F2 ®...®(Fn-1 ®(Fn ® F))...).
Для доказательства достаточности предположим, что ├─ F 1 ®(F 2 ® (...(Fn ® F)...)). Воспользуемся утверждением 2, получим F 1 ├─ F 1 ®(F 2 ® (...(Fn ® F)...)). По правилу заключения получаем F 1 ├─ F 2 ®(F 3 ® (...(Fn ® F)...)). Затем через получим 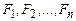 ├─ F. Теорема доказана.
├─ F. Теорема доказана.
Таким образом, благодаря следствию проверка выводимости формулы F из формул 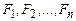 сводится к проверке доказуемости формулы F 1 ®(F 2 ® (...(Fn ® F)...)).
сводится к проверке доказуемости формулы F 1 ®(F 2 ® (...(Fn ® F)...)).
С помощью теоремы дедукции можно получать новые правила исчисления высказываний.
Пример. Рассмотрим формулы
X ® (Y ® Z), Y, X.
Применяя два раза правило заключения, находим, что
X ® (Y ® Z), Y, X ├─ Z.
Применяя теорему дедукции, получим правило
├─ (X ® (Y ® Z)) ® (Y ® (X ® Z)),
которое носит название правила перестановки посылок.
Замечание. Формулы исчисления высказываний можно интерпретировать как формулы алгебры высказываний. Для этого свободные переменные исчисления высказываний будем трактовать как переменные алгебры высказываний, то есть переменные, принимающие значения «истина» или «ложь». Операции 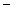 , Ù, Ú, ® определим также, как в алгебре высказываний. Тогда всякая формула при любых значениях переменных сама будет принимать одно из значений «истина» или «ложь», вычисляемое по правилам алгебры высказываний.
, Ù, Ú, ® определим также, как в алгебре высказываний. Тогда всякая формула при любых значениях переменных сама будет принимать одно из значений «истина» или «ложь», вычисляемое по правилам алгебры высказываний.
Теорема (о полноте исчисления высказываний). Формула F доказуема тогда и только тогда, когда F тождественно истинна.
Таким образом, для того чтобы установить, доказуема ли формула, достаточно составить ее таблицу истинности. Как известно, существует алгоритм построения таблицы истинности, и, значит, исчисление высказываний разрешимо.
Для проверки тождественной истинности аксиом рассмотри, например, таблицу истинности для аксиомы 8:
├─(X ® Z)®((Y ® Z)®(X Ú Y ® Z)).
| Х | Y | Z | 1Ú 2 | 1®3 | 2®3 | 4®3 | 6®7 | 5®8 |
Логическое исчисление называется непротиворечивым, если в нем не выводимы никакие две формулы, из которых одна является отрицанием другой. Иными словами, непротиворечивое исчисление – это такое исчисление, что какова бы ни была формула F, никогда формулы F и 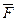 не могут быть одновременно выведены из аксиом этого исчисления с помощью указанных в нем правил. Проблема непротиворечивости состоит в следующем: является ли данное исчисление непротиворечивым или нет?
не могут быть одновременно выведены из аксиом этого исчисления с помощью указанных в нем правил. Проблема непротиворечивости состоит в следующем: является ли данное исчисление непротиворечивым или нет?
Для исчисления высказываний можно показать, что все аксиомы являются тождественно истинными формулами, а применяя к тождественно истинным формулам правила вывода, получим также тождественно истинные формулы. Следовательно, все выводимые формулы исчисления высказываний, рассматриваемые как формулы алгебры высказываний, являются тождественно истинными, что показывает непротиворечивость исчисления высказываний.
Теорема (о непротиворечивости исчисления высказываний). Исчисление высказываний непротиворечиво.
Доказательство. По теореме о полноте любая формула, не являющаяся тождественно истинной, не доказуема в исчислении высказываний. Например, такой формулой является формула 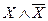 .
.
Однако возникает обратный вопрос: будет ли всякая тождественно истинная формула алгебры высказываний выводима в исчислении высказываний? Этот вопрос представляет собой проблему полноты в широком смысле для исчисления высказываний. Смысл этой постановки вопроса состоит в том, что при построении логического исчисления, предназначенного выражать содержательную логику, нам требуется знать, достаточно ли мы имеем аксиом и правил для того, чтобы вывести любую формулу, которая в содержательном понимании является тождественно истинной. Проблема полноты в широком смысле решается положительным образом: всякая тождественно истинная формула алгебры высказываний выводима в исчислении высказываний.
Не менее важное значение, чем понятие полноты в широком смысле, имеет понятие полноты логического исчисления в узком смысле. Логическое исчисление называется полным в узком смысле, если присоединение к ее аксиомам какой-нибудь не выводимой в ней формулы приводит к противоречию. Для исчисления высказываний проблема полноты в узком смысле также решается положительно.
 2015-04-12
2015-04-12 2558
2558
