Определим некоторые канонические представления ПФ.
ПФ называется элементарной конъюнкцией (конъюнктом), если она является конъюнкцией переменных и отрицаний переменных (конъюнкцией литер).
ПФ называется элементарной дизъюнкцией (дизъюнктом), если она является дизъюнкцией переменных и отрицаний переменных (дизъюнкцией литер).
Пример.
Говорят, что ПФ задана в дизъюнктивной нормальной форме (ДНФ), если она является дизъюнкцией элементарных конъюнкций.
Пример. 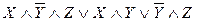 – ДНФ.
– ДНФ.
Говорят, что ПФ задана в конъюнктивной нормальной форме (КНФ), если она является конъюнкцией элементарных дизъюнкций.
Пример. 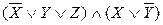 – КНФ.
– КНФ.
На основе равносильных преобразований любая формула может быть приведена к нормальной форме (ДНФ или КНФ) [3,4].
Алгоритм приведения ПФ к нормальным формам описывает следующая последовательность шагов.
Шаг 1. Если ПФ содержит операции → и ↔, то их исключить с помощью равносильностей
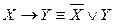 ,
, 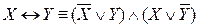 .
.
Шаг 2. Привести отрицания к независимым переменным, используя законы де Моргана.
Шаг 3. Раскрыть скобки по дистрибутивному закону конъюнкции относительно дизъюнкции для приведения к ДНФ или по дистрибутивному закону дизъюнкции относительно конъюнкции для приведения к КНФ.
Пример. Определить нормальные формы для ПФ 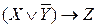 .
.
Действуя, в соответствии с алгоритмом, получим 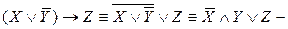 ДНФ.
ДНФ.
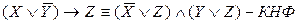
Применяя к полученной ДНФ дистрибутивный закон дизъюнкции относительно конъюнкции, получим
Замечание. Для данной ПФ существует множество ДНФ и КНФ, переход от одной формы к другой осуществляется на основе равносильных преобразований.
Совершенной дизъюнктивной нормальной формой (СДНФ) данной ПФ называется ДНФ, в которой каждая элементарная конъюнкция содержит все переменные – без отрицания или с отрицанием, но не вместе.
Совершенной конъюнктивной нормальной формой (СКНФ) данной ПФ называется КНФ, в которой каждая элементарная дизъюнкция содержит все переменные – без отрицания или с отрицанием, но не вместе.
Существует два способа перехода к совершенным формам аналитический и табличный [2, 3, 4].
Аналитический способ приведения ПФ к СДНФ осуществляется на основании равносильных преобразований и представляется следующей последовательностью шагов.
Шаг 1. С помощью равносильных преобразований привести ПФ к ДНФ.
Шаг 2. Те элементарные конъюнкции, в которые сомножителями входят не все переменные, умножить на единицы, представленные в виде дизъюнкций каждой недостающей переменной с ее отрицанием.
Шаг 3. Раскрыть скобки по соответствующему дистрибутивному закону.
Шаг 4. Для получения искомой СДНФ исключить повторения.
Замечание. Приведение к СКНФ осуществляется аналогично, но только к элементарным дизъюнкциям, содержащим слагаемыми не все переменные, прибавляют нули, представленные в виде конъюнкций каждой недостающей переменной с ее отрицанием.
Пример. Пусть ПФ, содержащая переменные X, Y, Z, имеет ДНФ вида 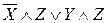 . Используя аналитический способ привести к СДНФ.
. Используя аналитический способ привести к СДНФ.
Заметим, что в первую элементарную конъюнкцию не входит переменная Y, а во вторую – переменная Х. В соответствии с процедурой приведения к СДНФ первую элементарную конъюнкцию умножим на 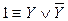 , а вторую – на
, а вторую – на 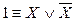 . Получим
. Получим
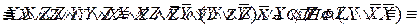
Приведение ПФ к СДНФ можно осуществить, используя таблицу истинности. Для этого надо выполнить следующую последовательность шагов.
Шаг 1. Составить таблицу истинности данной ПФ.
Шаг 2. Рассмотреть те строки, в которых формула принимает истинностное значение 1. Каждой такой строке поставить в соответствие элементарную конъюнкцию, причем переменная, принимающая значение 1, входит в нее без отрицания, а 0 – с отрицанием.
Шаг 3. Образовать дизъюнкцию всех полученных элементарных конъюнкций, которая и составит СДНФ.
Используя таблицу истинности, можно составить СКНФ для ПФ. Для этого надо выполнить следующую последовательность шагов.
Шаг 1. Составить таблицу истинности данной ПФ.
Шаг 2. Рассмотреть те строки, в которых формула принимает истинностное значение 0. Каждой такой строке поставить в соответствие элементарную дизъюнкцию, причем переменная, принимающая значение 1, входит в нее с отрицанием, а 0 – без отрицания.
Шаг 3. Образовать конъюнкцию всех полученных элементарных дизъюнкций, которая и составит СКНФ.
Пример.Привести ПФ 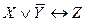 к совершенным нормальным формам. Для приведения к совершенным нормальным формам воспользуемся табличным способом. Построим таблицу истинности и на ее основе составим СДНФ и СКНФ.
к совершенным нормальным формам. Для приведения к совершенным нормальным формам воспользуемся табличным способом. Построим таблицу истинности и на ее основе составим СДНФ и СКНФ.
| X | Y | Z | 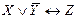 | Элементарные конъюнкции | Элементарные дизъюнкции |
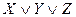 | |||||
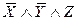 | |||||
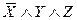 | |||||
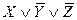 | |||||
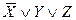 | |||||
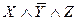 | |||||
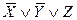 | |||||
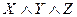 |
СДНФ:
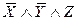
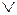
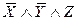
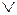
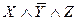
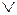
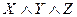
СКНФ:
(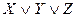 )
) 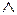 (
(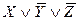 )
) 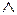 (
(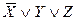 )
) 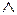 (
(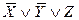 )
)
Заметим, что из табличного способа построения совершенных нормальных форм следует, что тождественно ложные формулы не имеют СДНФ; тождественно истинные формулы не имеют СКНФ. Для выполнимых ПФ справедливы следующие теоремы:
Теорема 1.1.5.1. Если ПФ имеет СДНФ, то она единственна.
Теорема 1.1.5.2. Если ПФ имеет СКНФ, то она единственна.
Единственность совершенных нормальных форм у выполнимой ПФ обуславливает их использование для доказательства равносильностей, идея которого состоит в следующем: если у двух ПФ их СДНФ (СКНФ) совпадают, то они равносильны.
 2015-04-12
2015-04-12 1475
1475

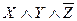 –
–  –
–