2015-04-12
4233
В общем случае метод резолюций неэффективен, так как количество переборов, которые необходимо сделать для получения ответа, экспоненциально зависит от количества информации (числа дизъюнктов и переменных), содержащейся в множестве дизъюнктов. Однако для некоторых классов дизъюнктов, к которым относится класс хорновских дизъюнктов, метод резолюций эффективен.
Дизъюнкт D называется хорновским, если он содержит не более одной переменной без отрицания (позитивной переменной).
Пример. Хорновскими дизъюнктами являются следующие дизъюнкты: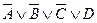 
, 
, 
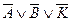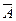, В.
В общем случае хорновские дизъюнкты имеют вид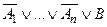 
(что равносильно формуле 
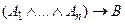) или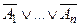 
. Хорновский дизъюнкт вида 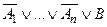называется точным. При этом переменные А 1, …, Аn называются фактами, а переменная В – целью. Хорновский дизъюнкт вида 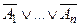называется негативным. Дизъюнкт D = B называется унитарным позитивным дизъюнктом.
Если S – множество хорновских дизъюнктов, то невыполнение множества S проверяется следующим образом. Выбирается в S унитарный позитивный дизъюнкт Р и дизъюнкт D из S, содержащий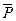 
. После этого заменяем S на (S \ { D })È{ res (D, P)} и продолжаем процесс до тех пор, пока S не будет содержать 0. Если на заключительном шаге множество дизъюнктов будет содержать 0, то исходное множество S противоречиво, в противном случае S непротиворечиво.
Пример. Проверить на противоречивость множество дизъюнктов
.
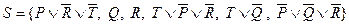Для доказательства противоречивости запишем дизъюнкты из S в таблицу и применим описанные алгоритм, записывая результат каждого следующего шага в таблицу. Переменные, использующиеся на данном шаге, будем подчеркивать.
| Номер шага | 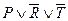 | 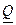 | R |  |  |  |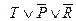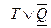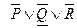
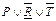 | Q | R | 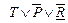 | T |  | |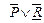
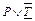 | Q | R | 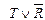 | T |  | |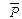
| P | Q | R | 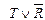| T | | |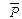
На шаге 4 получаем 0, являющийся резолютивным выводом из S. Следовательно, множество S невыполнимо.
