16 Понятие средних величин. Основные положения теории средних величин.
Средняя величина - показатель, который характеризует обобщенное значение признака или группы признаков в исследуемой совокупности.
Средняя величина отражает то общее, что присуще всем единицам исследуемой совокупности.
Если индивидуальные значения признака заменить средней величиной, то общий объем признака не измениться
Основные положения теории средних величин.
1. Индивидуальные значения, из которых исчисляются средние, должны относится к однородной совокупности, а число их должно быть значительным.
2. Метод средних величин должен сочетаться с методом группировок.
3. Необходимо рассчитывать внутригрупповые средние.
В статистике используют различные виды средних величин. Выбор той или иной средней зависит от содержания осредняемого признака и конкретных данных, по которым ее приходится вычислять.
17,18 Средняя арифметическая простая и взвешенная.
Средняя арифметическая используется для определения среднего уровня изучаемого признака, когда исходные данные представлены рядом распределения.
Средняя арифметическая простая используется, когда расчет осуществляется по несгруппированным статистическим данным, где нужно получить среднее слагаемое или частоты ряда распределения равны между собой.
Пример № 1
Найти среднюю выработку рабочих бригады, если известны следующие данные о выработке:
| Табельный номер рабочего | |||||
| Выработка, шт/час (xi) |
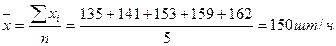 ,
,
где n – число вариант.
Средняя арифметическая взвешенная применяется при расчете средних величин, значения которых могут повторяться, поэтому расчет средней величины производится по сгруппированным данным (т.е. если частоты не равны между собой).
Пример 2
Определите среднюю заработную плату в 2000г.
| Цех | 2000г. | 2001г. | ||
| Заработная плата в среднем по цеху, руб. (x) | Число рабочих, чел. (f) | Заработная плата в среднем по цеху, руб. (x) | Фонд оплаты труда, руб. (M) | |
| №1 | ||||
| №2 | ||||
| №3 | ||||
| Итого | - | - |
: 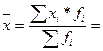
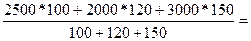 2540,5 руб.
2540,5 руб.
Следовательно, средняя заработная плата в 2000г. по всей совокупности работников составляла 2540,5 руб.
Частные случаи расчета средней арифметической
1. Средняя арифметическая интервального ряда распределения.
Пример 3
| Возраст, лет | До 25 | 25-35 | 35-45 | 45-55 | 55-65 | Свыше 65 |
| Число рабочих |
Определить средний возраст рабочих.
Для преобразования непрерывного ряда в дискретный определим середины каждого интервала. При этом величина каждого открытого интервала приравнивается к величине смежного интервала.
| Возраст, лет (открытые интервалы) | Возраст, лет (закрытые интервалы) | Середина интервала (xi) | Число рабочих (fi) | xi*fi | Накопленная частота |
| До 25 | 15-25 | ||||
| 25-35 | 25-35 | 10+20=30 | |||
| 35-45 | 35-45 | 10+20+50=80 | |||
| 45-55 | 45-55 | ||||
| 55-65 | 55-65 | ||||
| Свыше 65 | 65-75 | ||||
| Итого | - | - | - |
Вычислим среднюю по формуле средней арифметической взвешенной: 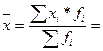
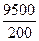 =47,5 лет. Таким образом, средний возраст рабочих – 47,5 лет.
=47,5 лет. Таким образом, средний возраст рабочих – 47,5 лет.
2. Средняя арифметическая из относительных величин.
В данном случае за варианты принимают сами относительные величины, за частоты – основание относительной величины.
3. Средняя арифметическая из групповых средних величин
В данном случае за варианты принимают групповые средние величины, за частоты – численность групп.
20 Средняя гармоническая простая и взвешенная.
Средняя гармоническая используется в случаях, кода неизвестны частоты (fi), а известен объем изучаемого признака (xi*fi=Mi).
По примеру 2 определим среднюю заработную плату в 2001г.
В исходной информации 2001г. нет данных о количестве работников, однако ее нетрудно рассчитать как отношение фонда оплаты труда к средней зарплате.
Тогда 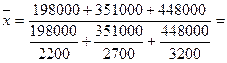 2769,4 руб., т.е. средняя зарплата в 2001г. –2769,4 руб.
2769,4 руб., т.е. средняя зарплата в 2001г. –2769,4 руб.
В данном случае использована средняя гармоническая: 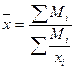 ,
,
где Мi –фонд оплаты труда в отдельном цеху; xi –зарплата в отдельном цеху.
Следовательно, средняя гармоническая применяется тогда, когда неизвестен один из сомножителей, но известно произведение «М».
Средняя гармоническая используется для расчета средней производительности труда, среднего процента выполнения норм, средней зарплаты и т.д.
Если произведения «М» равны между собой, то используется средняя гармоническая простая: 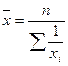 , где n – число вариант.
, где n – число вариант.
22 Средняя геометрическая и средняя хронологическая.
Средняя геометрическая используется для анализа динамики явлений и позволяет определить средний коэффициент роста. При расчете средней геометрической индивидуальные значения признака обычно представляют собой относительные показатели динамики, построенные в виде цепных величин, как отношения каждого уровня ряда к предыдущему уровню.
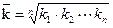 ,
, 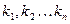 - цепные коэффициенты роста;
- цепные коэффициенты роста;
n – число цепных коэффициентов роста.
Если исходные данные даны по состоянию на определенные даты, то средний уровень признака определяется по формуле средней хронологической. Если промежутками между датами (моментами) равные, то средний уровень определяется по формуле средней хронологической простой..
Рассмотрим ее расчет на конкретных примерах.
Пример. Имеются следующие данные об остатках вкладов населения в банках России в первом полугодии 1997 г. (на начало месяца):
| Месяц | |||||||
| Сумма вкладов у, трлн руб. | 127,6 | 129,7 | 132,7 | 133,8 | 135,4 | 137,1 | 139,8 |
Средний остаток вкладов населения за первое полугодие 1997 г. (по формуле средней хронологической простой) составил:
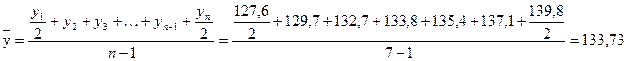 трлн руб.
трлн руб.
n – число дат.
В случае неравных промежутков между датами среднюю хронологическую можно рассчитать как среднюю арифметическую из средних значений уровней на каждую пару моментов, взвешенных по величине расстояний (отрезков времени) между датами.
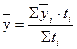 ,
,
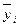 - средний уровень изучаемого признака в i-том периоде;
- средний уровень изучаемого признака в i-том периоде;
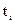 - продолжительность i-того периода.
- продолжительность i-того периода.
Пример. Пусть имеются следующие данные о наличии товарных остатков на складе за 1997 г.:
| Дата учета | 01.01.97 | 01.03.97 | 01.06.97 | 01.11.97 | 01.01.98 |
| Остатки товаров у, тыс. руб. |
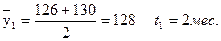
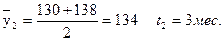
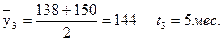
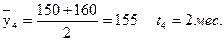
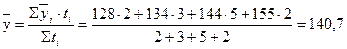 тыс. руб.
тыс. руб.
23,24 Понятие моды и медианы.
В случаях, когда использование средней арифметической невозможно или нецелесообразно используются структурные средние: мода и медиана.
Мода - наиболее типичное, чаще всего встречаемое значение признака.
Мода – это варианта, которая наиболее часто встречается в данном ряду распределения, т.е. имеет наибольшую частоту.
В случаях интервальных рядов с равными интервалами, модальным интервалом считается интервал с наибольшей частотой, а при неравных интервалах — интервал с наибольшей плотностью.
В интервальном ряду распределения мода определяется по формуле:
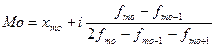 , где
, где
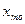 - нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту, в данном примере это интервал 45-55, имеющий наибольшую частоту в ряде распределения 70),
- нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту, в данном примере это интервал 45-55, имеющий наибольшую частоту в ряде распределения 70),
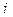 - величина модального интервала (в нашем примере
- величина модального интервала (в нашем примере 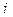 =55-45=10),
=55-45=10),
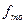 - частота модального интервала,
- частота модального интервала,
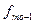 - частота интервала, предшествующего модальному,
- частота интервала, предшествующего модальному,
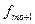 - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным.
Пример 3
| Возраст, лет (открытые интервалы) | Число рабочих (fi) |
| До 25 | |
| 25-35 | |
| 35-45 | 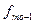 = 50 = 50 |
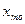 =45-55 =45-55 | 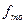 = 70 = 70 |
| 55-65 | 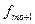 = 30 = 30 |
| Свыше 65 | |
| Итого |
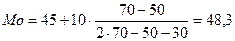 лет.
лет.
Т.е. чаще всего встречается возраст рабочих 48,3 лет.
Медиана - значение варьирующего признака, приходящееся на середину ранжированной совокупности.
Ранжированным называется ряд распределения, построенный в прядке возрастания или убывания признака
При исчислении медианы интервального ряда сначала находится интервал, содержащий медиану. Медианному интервалу соответствует первый из интервалов, для которых накопленная сумма частот превышает половину общей совокупности наблюдений.
В интервальном ряду распределения медиана определяется по формуле:
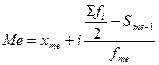 , где
, где
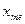 - нижняя граница медианного интервала (в нашем примере это интервал 45-55, т.к. накопленная частота этого интервала близка по значению к полусумме накопленных частот)
- нижняя граница медианного интервала (в нашем примере это интервал 45-55, т.к. накопленная частота этого интервала близка по значению к полусумме накопленных частот)
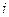 - величина медианного интервала,
- величина медианного интервала,
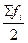 - полусумма накопленных частот (в нашем примере:
- полусумма накопленных частот (в нашем примере: 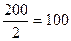 ),
),
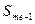 - накопленная частота интервала, предшествующего медианному.
- накопленная частота интервала, предшествующего медианному.
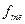 - частота медианного интервала.
- частота медианного интервала.
| Возраст, лет (открытые интервалы) | Число рабочих (fi) | Накопленная частота |
| До 25 | ||
| 25-35 | 10+20=30 | |
| 35-45 | 10+20+50=80= 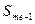 | |
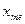 = 45-55 = 45-55 | 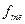 =70 =70 | |
| 55-65 | ||
| Свыше 65 | ||
| Итого | - |
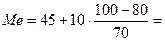 47,9 лет. Т.е. половина рабочих имеет возраст до 47,9 лет, а половина выше.
47,9 лет. Т.е. половина рабочих имеет возраст до 47,9 лет, а половина выше.
25-29 Понятие и показатели вариации.
Вариация - это колеблемость значений признака в совокупности.
1 Размах вариации – разность между максимальным и минимальным значением признака в совокупности.
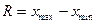
Недостаток – при расчете учитывают только крайние значения, вызванные аномальными причинами
2 Среднее линейное отклонение – средняя арифметическая из отклонение вариант от средней арифметической, взятое без учета знака этих отклонений.
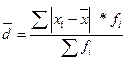
Показывает, на сколько в среднем отклоняется значения изучаемого признака от средней арифметической.
Недостаток – использование модуля.
3 Дисперсия - квадрат стандартного отклонения. Этот показатель несет ту же информацию, что и стандартное отклонение, но труднее интерпретируется, поскольку единица измерения дисперсии представляют собой единицы измерения исходных данных, возведенных в квадрат.
s2= 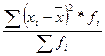
4 Среднее квадратическое отклонение - это положительный квадратный корень дисперсии. Оно определяется выборочным среднеквадратическим отклонением, которое представляет собой положительный квадратный корень выборочной дисперсии.
s = 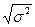
Показывает, на сколько в среднем отклоняется значения изучаемого признака от средней арифметической.
5 Коэффициент вариации - это отношение совокупного среднеквадратического отклонения к среднему значению
V= 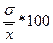
Если коэффициент вариации менее 33%, то совокупность считается однородной.
С помощью коэффициента вариации можно сравнить колеблемость одного и того же признака в разных совокупностях или вариации различных признаков в одной совокупности.
Рассчитаем показатели вариации – дисперсию, среднее линейное отклонение, среднее квадратическое отклонение (стандартное отклонение) и коэффициент вариации, используя данные задачи №3.
| Возраст, лет | Середина интервала (xi) | Число рабочих (f) | |xi- 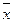 | | | |xi- 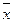 |*f |*f | |
| До 25 | |20-47,5|=27,5 | ||||
| 25-35 | 17,5 | ||||
| 35-45 | 7,5 | ||||
| 45-55 | 2,5 | ||||
| 55-65 | 12,5 | ||||
| Свыше 65 | 22,5 | ||||
| Итого | - | - |
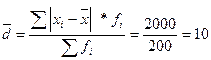
В среднем возраст работников отклоняется от среднего возраста 47,5 лет на 10 лет.
s2= 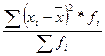
| Возраст, лет | Середина интервала (x) | Число рабочих (f) | (xi- 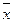 ) ) | (xi- 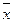 )2 )2 | (xi- 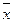 )2*f )2*f |
| До 25 | -27,5 | 756,25 | 7562,5 | ||
| 25-35 | -17,5 | 306,25 | 6125,0 | ||
| 35-45 | -7,5 | 56,25 | 2812,5 | ||
| 45-55 | 2,5 | 6,25 | 437,5 | ||
| 55-65 | 12,5 | 156,25 | 4687,5 | ||
| Свыше 65 | 22,5 | 506,25 | 10125,0 | ||
| Итого | - | - | - | 31750,0 |
Тогда s2= 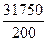 =158,75
=158,75
Среднее квадратическое отклонение: s = 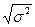 =
= 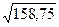 =12,6.
=12,6.
Коэффициент вариации: V= 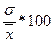 =12,6/47,5*100=26,5%.
=12,6/47,5*100=26,5%.
В среднем возраст работников отклоняется от среднего возраста 47,5 лет на 12,6 лет. Так как коэффициент вариации меньше 33%, то делаем вывод о статистической однородности совокупности. В противном случае необходимо разбивать совокупность на группы и все расчеты делать для каждой группы в отдельности.
По данным примера 6 темы «Сводка и группировка» оцените тесноту связи между изучаемыми признаками, рассчитав коэффициент детерминации эмпирическое корреляционное отношение.
Межгрупповая дисперсия вычисляется по формуле:
d2= 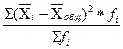 , где:
, где:
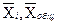 – соответственно средняя i -й группы и общая средняя;
– соответственно средняя i -й группы и общая средняя;
fi – объем i–й группы (межгруппавая дисперсия рассчитывается для результативног о признака)
Для определения межгрупповой дисперсии произведем расчеты в таблице:
| Группы предприятий | Количество предприятий fi | Сумма затрат на перевозку, тыс. руб. в среднем на 1 предприятие, тыс. руб. Xi | 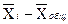 | 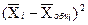 | 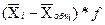 |
| 15-32 | 701,1 | -280,4 | 78624,16 | 786241,6 | |
| 32-49 | 1082,0 | 120,3 | 14472,09 | 72360,45 | |
| 49-66 | 1440,8 | 440,5 | 194040,25 | 970201,25 | |
| Итого | 1000,3 | - | - | 1828803,3 |
d2= 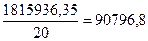
Средняя из внутригрупповых дисперсии рассчитывается по формуле:
s2= 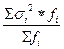 где
где
s2i -внутригрупповая дисперсия i-й группы, которая рассчитывается отдельно для каждой группы:
Для 1 группы:
| Номера предприятий | Сумма затрат на перевозку, т. р.. | (Xi- 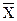 i); i); 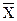 i=701,1 i=701,1 | (Xi- 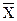 i)2 i)2 |
| -229,1 | 52486,81 | ||
| 48,9 | 2391,21 | ||
| 138,9 | 19293,21 | ||
| 102,9 | 10588,41 | ||
| 22,9 | 524,41 | ||
| -122,1 | 14908,41 | ||
| -2,1 | 4,41 | ||
| -89,1 | 7938,81 | ||
| 128,9 | 16615,21 | ||
| Итого | - | 124750,89 |
s21= 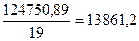
Для 2 группы
| Номера предприятий | Сумма затрат на перевозку, т. р. | (Xi- 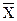 i); i); 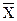 i=1082 i=1082 | (Xi- 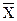 i)2 i)2 |
| -2 | |||
| -49 | |||
| -193 | |||
| Итого | - |
s22= 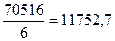
Для 3 группы
| Номера предприятий | Сумма затрат на перевозку, т. р. | (Xi- 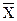 i); i); 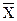 i=1440,8 i=1440,8 | (Xi- 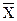 i)2 i)2 |
| 109,2 | 11924,64 | ||
| -130,8 | 17108,64 | ||
| 3,2 | 10,24 | ||
| 59,2 | 3504,64 | ||
| -40,8 | 1664,64 | ||
| Итого | 34212,8 |
s23= 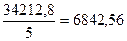
Рассчитаем среднюю из внутригрупповых:
s2= 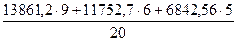 =11474
=11474
По правилу сложения дисперсий общая дисперсия равна сумме межгрупповой дисперсии и средней из внутригрупповых дисперсий:
s2общ= d2+s2
s2общ=90796,8+11474=102270,8
Отношение межгрупповой дисперсии к общей называется коэффициентам детерминации:
h2= 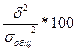
h2= 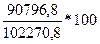 =88,8%
=88,8%
Это означает, что вариация суммы затрат на перевозку на 89,4% зависит от грузооборота, а на 10,6% от остальных факторов.
Квадратный корень из коэффициента детерминации называется эмпирическое корреляционное отношение и характеризует силу связи между изучаемыми факторами:
h= 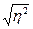
h= 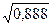 =0,94
=0,94
Согласно шкале связь между грузооборотом и суммой затрат весьма высокая.
 2015-04-12
2015-04-12 1179
1179








