1). Составить каноническое уравнение эллипса, если:
а) 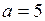 ,
, 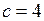 ; б)
; б) 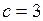 ,
, 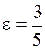 ; в)
; в) 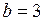 ,
, 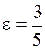 ; г) большая полуось равна 3, а расстояние между фокусами равно
; г) большая полуось равна 3, а расстояние между фокусами равно 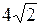 , д) эллипс проходит через точки
, д) эллипс проходит через точки 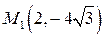 и
и 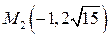 .
.
2) Составить каноническое уравнение гиперболы, если:
а) 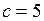 ,
, 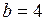 ; б)
; б) 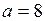 ,
, 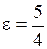 ; в)
; в) 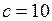 ,
, 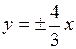 – уравнения асимптот; г) мнимая полуось равна 1, а расстояние между фокусами равно
– уравнения асимптот; г) мнимая полуось равна 1, а расстояние между фокусами равно 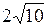 .
.
3) Написать каноническое уравнение параболы с вершиной в точке (0,0), если:
а) она расположена в левой полуплоскости, симметрична относительно оси Ох и 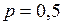 ;
;
б) если она симметрична относительно оси Оу и походит через точку М (4,–8);
в) если точка F (0,3) – фокус.
4) Найти радиус и координаты центра окружности:
а) 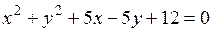 ; б)
; б) 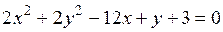 ,
,
в) 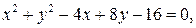 г)
г) 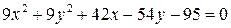 .
.
5) Определить вид кривой второго порядка, заданной уравнением, найти ее центр, координаты вершин, фокусов и эксцентриситет:
а) 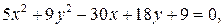 б)
б) 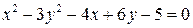 ,
,
в) 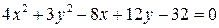 , г)
, г) 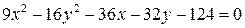 .
.
6) Дано уравнение эллипса 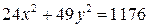 . Найти: длины его полуосей, координаты фокусов, эксцентриситет эллипса, уравнение директрис и расстояние между ними, точки эллипса, расстояние от которых до левого фокуса равно 12.
. Найти: длины его полуосей, координаты фокусов, эксцентриситет эллипса, уравнение директрис и расстояние между ними, точки эллипса, расстояние от которых до левого фокуса равно 12.
7) Дано уравнение гиперболы 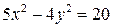 . Найти: длины его полуосей, координаты фокусов, эксцентриситет гиперболы, уравнения асимптот и директрис, фокальные радиусы точки
. Найти: длины его полуосей, координаты фокусов, эксцентриситет гиперболы, уравнения асимптот и директрис, фокальные радиусы точки 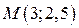 .
.
8) Найти координаты вершины и фокуса, уравнение оси и директрисы параболы
а) 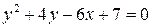 , б)
, б) 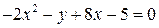 .
.
 2015-04-12
2015-04-12 296
296








