Задания для практических занятий по теме «Аналитическая геометрия»
Прямая на плоскости
1) Среди прямых 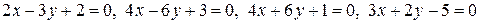 указать параллельные и перпендикулярные.
указать параллельные и перпендикулярные.
2) Прямая 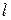 задана точкой
задана точкой 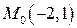 и нормальным вектором
и нормальным вектором 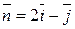 . Составить уравнение этой прямой и привести его к общему виду.
. Составить уравнение этой прямой и привести его к общему виду.
3) Написать уравнение прямой, отсекающей на осях координат отрезки, величины которых соответственно равны 3 и 4.
4) Составить уравнение прямой, проходящей через точки 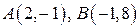 .
.
5) Определить угловой коэффициент 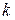 и отрезок
и отрезок 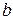 для каждой из прямых:
для каждой из прямых: 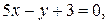
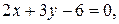
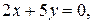
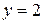 .
.
6) Найти уравнение прямой, образующей с осью 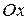 угол
угол 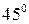 и пересекающей ось
и пересекающей ось 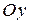 в точке
в точке 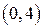 .
.
7) Найти расстояние от точки 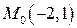 до прямой
до прямой 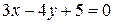 .
.
8) Записать уравнение прямой 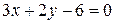 в отрезках, найти точки, в которых прямая пересекает оси координат.
в отрезках, найти точки, в которых прямая пересекает оси координат.
9) Определить острый угол между прямыми 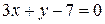 и
и 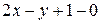 .
.
10) Составить уравнение прямой, проходящей через точку 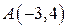 и параллельной прямой:
и параллельной прямой:
а) 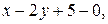 б)
б) 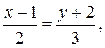 в)
в) 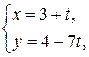 г)
г) 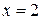 .
.
11) Установить, пересекаются, параллельны или совпадают данные прямые:
а) 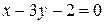 и
и 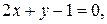 б)
б) 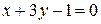 и
и 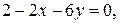
в) 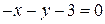 и
и 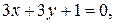 г)
г) 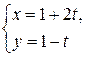 и
и 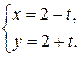
12) При каких значениях 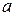 прямые
прямые 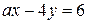 и
и 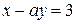 :
:
а) пересекаются, б) параллельны, в) совпадают?
13) Точки 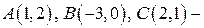 вершины треугольника
вершины треугольника 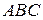 . Написать:
. Написать:
а) уравнение стороны 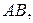 б) уравнение высоты
б) уравнение высоты 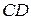 и вычислить ее длину, в) уравнение медианы
и вычислить ее длину, в) уравнение медианы 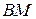 стороны
стороны 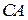 , г) найти угол
, г) найти угол 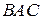 треугольника
треугольника 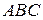 .
.
14) Составить уравнение прямой, проходящей через точку 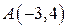 и перпендикулярной прямой:
и перпендикулярной прямой:
а) 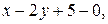 б)
б) 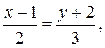 в)
в) 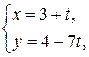 г)
г) 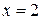 .
.
15) Найти расстояние от точки 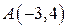 до прямой:
до прямой:
а) 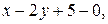 б)
б) 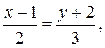 в)
в) 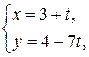 г)
г) 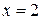 .
.
16) Найти угол между прямыми:
а) 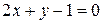 и
и 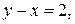 б)
б) 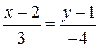 и
и 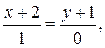
в) 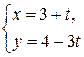 и
и 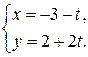
17) Дано общее уравнение прямой 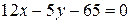 . Написать: а) уравнение с угловым коэффициентом, б) уравнение в отрезках, в) нормальное уравнение.
. Написать: а) уравнение с угловым коэффициентом, б) уравнение в отрезках, в) нормальное уравнение.
18) Определить площадь треугольника, образованного прямой 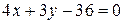 с осями координат.
с осями координат.
19) Показать, что прямые 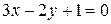 и
и 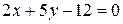 пересекаются, и найти координаты точки пересечения
пересекаются, и найти координаты точки пересечения
 2015-04-12
2015-04-12 395
395







