Пусть дана система АХ = В n линейных уравнений с n неизвестными. Если êAêне равно 0, то система имеет единственное решение:x1=êA1ê/ êA ê; x2=êA2ê/ êA, где Аi, Определители получаются из определителя|А| заменой соответствующего столбца столбцом свобод членов.
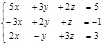
В виде матрицы эту систему можно записать таким образом:
A = 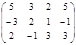 , где
, где
ответы будут уравнений будут находится в последнем столбце. Теперь мы введем понятие основного определителя; в данном случае он будет выглядеть таким образом:
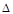 =
= 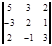 = 66.
= 66.
Основным определителем является матрица, составленная из коэффициентов стоящих при переменных. Они также идут в порядке столбцов, т. е. в первом столбце стоят коэффициенты, которые находятся при x, во втором столбце при y, и так далее. Это очень важно, ибо в следующих действиях мы заменяем каждый столбец коэффициентов при переменной на столбец ответов уравнений.
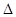 1 =
1 = 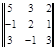 = 43,
= 43,
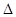 2 =
2 = 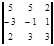 = 41,
= 41,
 3 =
3 = 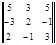 = 51.
= 51.
Затем нужно найти определители  1,
1,  2,
2, 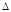 3 и применить правило Крамера. Оно выглядит так:
3 и применить правило Крамера. Оно выглядит так:
x1 = 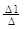 =
= 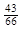 ,
,
x2 = 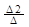 =
= 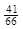 ,
,
x3 = 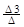 =
= 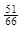 – для данного случая, а в общем виде оно выглядит следующим образом: xi =
– для данного случая, а в общем виде оно выглядит следующим образом: xi = 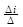 .
.
 2015-04-12
2015-04-12 431
431







