Собственные значения и собственные векторы матрицы

Определение 1: Число l называется собственным значением квадратной матрицы А порядка n x n, если найдется ненулевой вектор 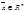, такой, что выполняется равенство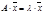

Рассуждения для собственных векторов:

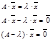
Получена система линейных однородных уравнений, которая должна иметь ненулевое решение, значит

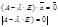
Обозначим эти равенства (4) и (5) соответственно.

Если раскрыть определитель из равенства (5), то получится многочлен n- ой степени относительно l. Этот многочлен будем называть характеристическим уравнением матрицы А.

Определение 2: Уравнение (5) называется характеристическим уравнением матрицы А.

Таким образом собственные значения матрицы А являются корнями ее характеристического уравнения.

Определение 3: Ненулевой вектор 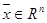называется собственным вектором квадратной матрицы А порядка n, принадлежащим ее собственному значению l, если 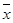является решением системы (4). Множество всех собственных векторов, принадлежащих собственному значению l, совпадает с множеством всех ненулевых решений системы

57. Как связаны собственные значения кв. матриц А и А^T.

Собственные значения матриц А и А^T совпадают. Док-во корни характеристического уравнения – λ. |A- λE|=0, |A(t)- λE|=0, |A(T)- λE|=0 харктеристическое уравнение от А(Т). решения этого уравнения явл. Собственные значения А(Т).