Решение. По теореме Крамера система линейных алгебраических уравнений имеет единственное решение тогда и только тогда

По теореме Крамера система линейных алгебраических уравнений имеет единственное решение тогда и только тогда, когда ее определитель отличен от нуля. При этом решение находится по формулам 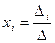, где ∆ - определитель системы, а ∆_i - определитель, получающийся из определителя сис­темы заменой i-ro столбца на столбец свободных членов.

1) Найдем определитель матрицы системы:

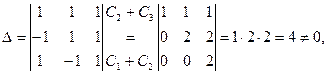
следовательно, система имеет единственное решение.

2) Теперь найдем определители ∆_1,∆_2,∆₃. Последовательно заменив в ∆, первый, второй и третий столбцы столбцом свободных членов, получим соответственно:

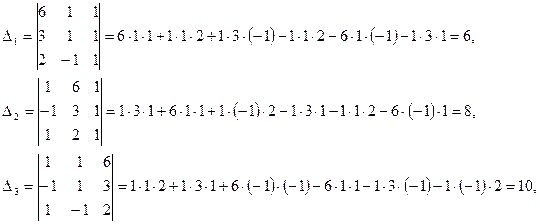
3) Вычислим неизвестные

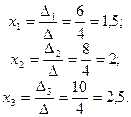
4) Сделаем проверку:

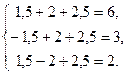
Получили систему верных равенств, следовательно, система решена верно.

Ответ:,,