Вариант №3
Задание № 1. Алгебра матриц
Вычислить:
1) Матрицу 2A-3B
2) Произведение матриц АВ и ВА. Выяснить, является ли данные матрицы перестановочными.
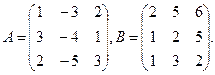
Решение.
1) Найдем 2А: 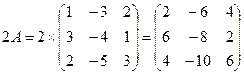
Найдем 3B: 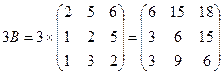
Вычисляем 2А-3В: 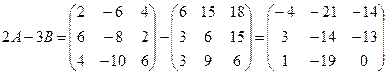 , тогда
, тогда
2) 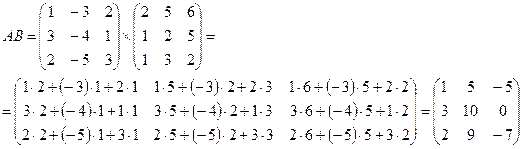
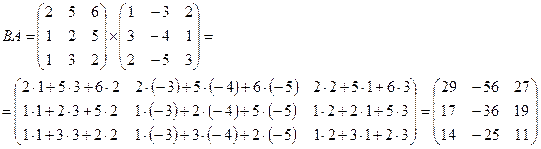
Так как АВ≠BA, то матрицы А и В не являются перестановочными.
Задание № 2. Определители
Вычислить определитель пятого порядка:
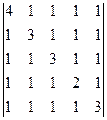
Решение.
Запишем матрицу в виде:
Преобразуем 1-ый столбец таким образом, чтобы в нем оказалось максимальное количество нулей.
Умножим 4-ую строку на (k = -1 / 1 = -1) и добавим к 5-ой:
| C5-C4 = | |||||
| -1 |
Умножим 3-ую строку на (k = -1 / 1 = -1) и добавим к 4-ой:
| C4-C3= | |||||
| -2 | |||||
| -1 |
Умножим 2-ую строку на (k = -1 / 1 = -1) и добавим к 3-ой:
| C3-C2 = | |||||
| -2 | |||||
| -2 | |||||
| -1 |
Умножим 1-ую строку на (k = -1 / 4 = -1/4) и добавим к 2-ой:
| C2-C1 = | |||||
| 11/4 | 3/4 | 3/4 | 3/4 | ||
| -2 | |||||
| -2 | |||||
| -1 |
Полученную матрицу разложим по элементам 1-ого столбца и преобразуем ее:
Добавим 4-ую строку к 3-ой:
| C3+C4= | 11/4 | 3/4 | 3/4 | 3/4 |
| -2 | ||||
| -2 | ||||
| -1 |
Добавим 3-ую строку к 4-ой:
| C4+C3 = | 11/4 | 3/4 | 3/4 | 3/4 |
| -2 | ||||
| -2 | ||||
| -2 | -1 |
Умножим 1-ую строку на (k = 2 / 11/4 = 8/11) и добавим к 2-ой:
| C2 +8/11C1 = | 11/4 | 3/4 | 3/4 | 3/4 |
| 28/11 | 6/11 | 6/11 | ||
| -2 | ||||
| -2 | -1 |
Полученную матрицу разложим по элементам первого столбца и преобразуем ее:
Умножим 2-ую строку на (k = -2 / 2 = -1) и добавим к 3-ой:
| C3-C2= | 28/11 | 6/11 | 6/11 |
| -2 | |||
| -1 |
Умножим 1-ую строку на (k = 2 / 28/11 = 11/14) и добавим к 2-ой:
| C2+11/14C1= | 28/11 | 6/11 | 6/11 |
| 3/7 | 17/7 | ||
| -1 |
Полученную матрицу разложим по элементам первого столбца и преобразуем ее:
Определитель равен ∆ = 4 * 11/4 * 28/11 * (3/7*2 - (-1)*17/7) = 92
Ответ: 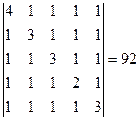
 2015-04-12
2015-04-12 1504
1504