2015-04-01
855
1 Предел отношения двух функций, в случае наличия неопределенност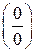и 
или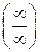 
, равен пределу отношения их производных (конечному или бесконечному), если последний предел существует:
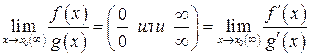. (5.12)
Таким образом, правило Лопиталя используется для раскрытия неопределенностей вида 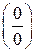или 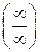. Если частное 
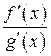вновь дает неопределенность 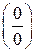или 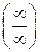, то можно перейти к отношению вторых производных и т.д.
В случае неопределенностей вида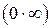 
или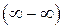 
следует путем алгебраических преобразований привести их к неопределенностям вида 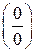или .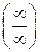
Задача 5.11. Найти предел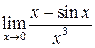 
.
Решение.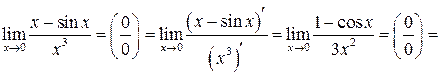 
.
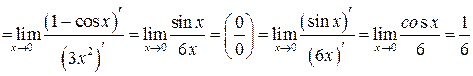В данном примере правило Лопиталя применялось три раза.
Пример 5.12. Требуется найти предел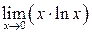 
.
Для нахождения предела произведения двух функций по правилу Лопиталя, представим данное произведение в виде частного двух функций:
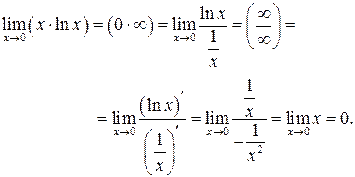
Задача 5.13. Найти предел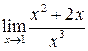 
.
Решение. При решении данной задачи никакой неопределенности не возникает, следовательно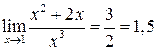 
. Если же этого не заметить и применить правило Лопиталя, то можно получить неверный результат:
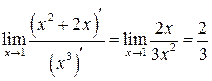. Таким образом правилом Лопиталя необходимо пользоваться осторожно, в строгом соответствии с его формулировкой.
