Пусть функция 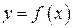 определена и имеет производные всех порядков до n -го включительно в некоторой окрестности
определена и имеет производные всех порядков до n -го включительно в некоторой окрестности 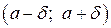 точки а. Тогда имеет место формула Тейлора:
точки а. Тогда имеет место формула Тейлора:
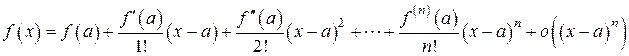 ,
,
где 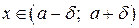 , а через
, а через 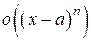 обозначена бесконечно малая величина более высокого порядка, чем
обозначена бесконечно малая величина более высокого порядка, чем 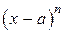 .
.
При а = 0 формула Тейлора получила называние формулы Маклорена:
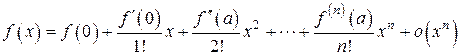 . (5.13)
. (5.13)
Хорошо известны разложения некоторых элементарных функций по формуле Маклорена:
1. 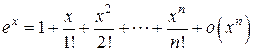 .
.
2. 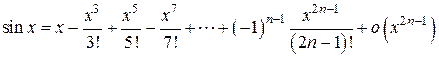 .
.
3. 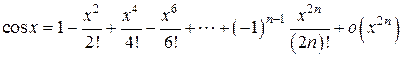 .
.
4. 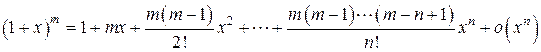 .
.
5. 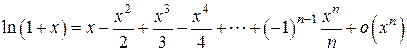 .
.
6. 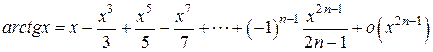 .
.
Пример 5.14. Разложить по формуле Маклорена функцию 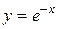 .
.
Подставляя – x вместо x в формулу Маклорена для функции 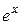 , получим искомое разложение:
, получим искомое разложение:
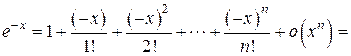
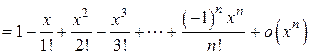 .
.
Задача 5.15. Написать три первых, отличных от тождественного нуля слагаемых формулы Маклорена для функции 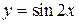 .
.
Решение. Подставляя 2 x вместо x в формулу Маклорена для функции 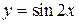 , получим
, получим
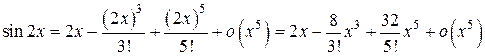 .
.
Таким образом, при достаточно малых x, многочлен 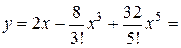
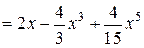 с точностью до бесконечно малой величины
с точностью до бесконечно малой величины 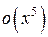 может заменить функцию
может заменить функцию 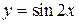 .
.
Задача 5.16. Разложить по степеням x – 2 многочлен
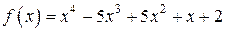 .
.
Решение. Найдем значения 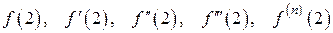 :
:
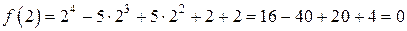 ,
,
img src="https://www.ok-t.ru/studopediaru/baza7/1445216852993.files/image1816.gif" alt="" />,
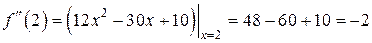 ,
,
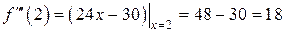 ,
, 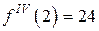 .
.
Остальные производные многочлена четвертой степени тождественно равны нулю. Подставляя найденные производные в формулу Тейлора, получим:
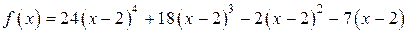 .
.
 2015-04-01
2015-04-01 17485
17485








