
Пусть точка x 0 входит в область определения функции
y = f (x) вместе с некоторой окрестностью. То есть, существует такое d > 0, что функция определена во всех точках, принадлежащих интервалу 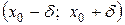 . Пусть
. Пусть 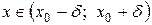 . Разность
. Разность
D x = x – x 0 называется приращением аргумента, а разность
D y = f (x) – f (x 0) = f (x 0+D x) – f (x 0) называется приращением функции в точке x 0 (см. рис. 5.1).
2 Производной функции y = f (x) в точке x 0 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
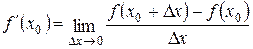 , (5.1)
, (5.1)
если предел (5.1) существует и конечен.
Предположим, что в некоторой окрестности 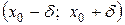 точки x 0 задана непрерывная функция y = f (x) (рис. 5.1). Значению x 0 соответствует точка А (x 0; y 0) на графике функции y = f (x). Придадим аргументу x 0 некоторое достаточно малое приращение D x, с таким расчетом, чтобы точка x 0 + D x не вышла за пределы окрестности:
точки x 0 задана непрерывная функция y = f (x) (рис. 5.1). Значению x 0 соответствует точка А (x 0; y 0) на графике функции y = f (x). Придадим аргументу x 0 некоторое достаточно малое приращение D x, с таким расчетом, чтобы точка x 0 + D x не вышла за пределы окрестности: 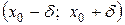 . Вычисляя значение функции в точке
. Вычисляя значение функции в точке
x = x 0 + D x, мы получим новую точку B (x 0 + D x; f (x 0 + D x)) на графике функции
y = f (x).
Прямая линия, проходящая через точки А и В, то есть пересекающая график функции не менее, чем в двух точках, называется секущей. Предположим, что секущая АВ составляет угол a = a (D x) с положительным направлением оси OX. Тогда, очевидно, что Ð ВАС = a.
Следовательно, угловой коэффициент секущей равен
kAB = 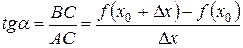 . Очевидно, что угловой коэффициент секущей, так же как и угол a ее наклона к оси OX зависит от D x.
. Очевидно, что угловой коэффициент секущей, так же как и угол a ее наклона к оси OX зависит от D x.
2 Касательной к графику функции y = f (x) в точке А (x 0; y 0) называется предельное положение секущей АВ при D x ® 0.
Так как при D x ® 0 точка В неограниченно приближается к точке А, то из данного определения следует, что касательная имеет с графиком функции только одну общую точку А в достаточно малой окрестности точки x 0. Если касательная к графику функции существует в точке А, то ее угол наклона b к оси OX (угол между касательной и положительным направлением оси OX) должен быть равен предельному положению угла наклона секущей к оси OX.
При этом угловой коэффициент касательной должен быть равен пределу углового коэффициента секущей при D x ® 0:
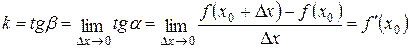 . (5.2)
. (5.2)
Суммируя сказанное, мы можем сделать следующий вывод. Если в некоторой точке x 0 функция y = f (x) имеет производную 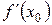 , то существует касательная к графику функции в точке А (x 0; y 0), причем угловой коэффициент данной касательной равен
, то существует касательная к графику функции в точке А (x 0; y 0), причем угловой коэффициент данной касательной равен 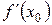 . В этом заключается геометрический смысл производной.
. В этом заключается геометрический смысл производной.
Уравнение касательной можно найти, используя уравнение (3.8) прямой, проходящей через заданную точку с заданным угловым коэффициентом:
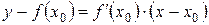 . (5.3)
. (5.3)
§5.2. Таблица производных
Пользуясь определением производной функции можно найти производные наиболее простых (элементарных) функций. Таким образом, мы получим таблицу производных, с помощью которой можно находить производные более сложных функций:
1. 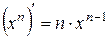 . 1¢.
. 1¢. 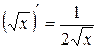 .
.
2. 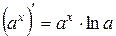 . 2¢.
. 2¢. 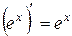 .
.
3. 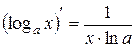 . 3¢.
. 3¢. 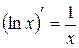 .
.
4. 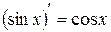 . 5.
. 5. 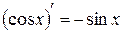 .
.
6. 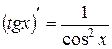 . 7.
. 7. 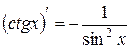 .
.
8. 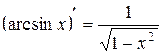 . 9.
. 9. 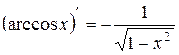 .
.
10. 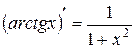 . 11.
. 11. 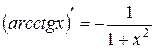 .
.
Выведем некоторые из табличных формул.
1. Производная степенной функции.
4 Воспользуемся формулой (4.9). Получим:
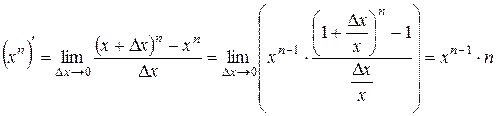 .3
.3
2. Производная показательной функции.
4 Воспользуемся формулой (4.8). Получим:
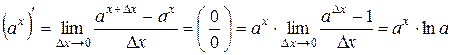 .3
.3
3. Производная функции 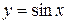 .
.
4 Воспользуемся формулой 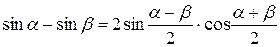 :
:
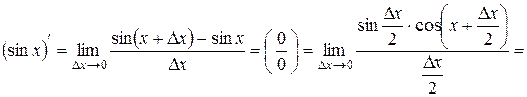 .
.
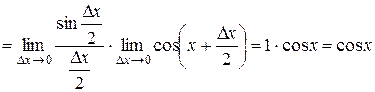 .3
.3
Аналогично выводится производная функции 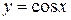 . Другие табличные производные будут выведены позднее.
. Другие табличные производные будут выведены позднее.
§5.3. Дифференциал функции, его геометрический смысл и применение в приближенных вычислениях
1. Дифференцируемость функции. Дифференциал.
Предположим, что функция y = f (x) определена на некотором интервале
(a, b).
2 Функция y = f (x) называется дифференцируемой в точке x 0Î(a, b), если ее приращение D y в этой точке можно представить в виде
D y = А ×D x + a (D x)×D x, (5.4)
где А – некоторая константа (не зависит от D x), а a (D x) – бесконечно малая величина при D x ® 0 (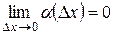 ).
).
2 Функция, дифференцируемая во всех точках некоторого множества (например, отрезка), называется дифференцируемой на данном множестве (отрезке).
Заметим, что второе слагаемое в правой части равенства (5.4) является бесконечно малой величиной более высокого порядка при D x ® 0 по сравнению с D x. Действительно, 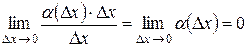 .
.
Первое слагаемое А ×D x (линейное относительно D x) при D x ® 0 является бесконечно малой величиной одного порядка с D x. То есть слагаемое А ×D x является главной частью приращения функции y = f (x) в точке x 0.
2 Главная, линейная относительно D x часть приращения функции y = f (x) в точке x 0 называется ее дифференциалом в точке x 0. Дифференциал функции обозначается символом dy. Таким образом, dy = А ×D x.
Докажем две теоремы, устанавливающие связь между дифференцируемостью и существованием производной в точке x 0, а так же между дифференцируемостью и непрерывностью функции в точке x 0.
g Для того, чтобы функция y = f (x) была дифференцируемой в точке x 0, необходимо и достаточно, чтобы она имела конечную производную в этой точке.
4 Необходимость. Пусть функция y = f (x) дифференцируема в точке x 0, то есть ее приращение D y в этой точке можно представить в виде (5.4). Разделив равенство (5.4) на D x, получим 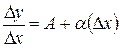 . Откуда
. Откуда 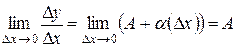 . Следовательно, производная функции y = f (x) в точке x 0 существует и равна А.
. Следовательно, производная функции y = f (x) в точке x 0 существует и равна А.
Достаточность. Пусть существует конечная производная f¢ (x 0), то есть 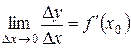 . Обозначая f¢ (x 0) через А, получим
. Обозначая f¢ (x 0) через А, получим 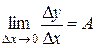 или
или 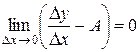 . То есть функция
. То есть функция 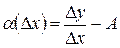 является бесконечно малой при D x ® 0. Умножая последнее равенство на D x, получим D y = А ×D x + a (D x)×D x. Следовательно, функция y = f (x) дифференцируема в точке x 0.3
является бесконечно малой при D x ® 0. Умножая последнее равенство на D x, получим D y = А ×D x + a (D x)×D x. Следовательно, функция y = f (x) дифференцируема в точке x 0.3
Из доказанной теоремы следует, что дифференциал функции y = f (x) в точке x 0 равен dy = f¢ (x 0)×D x. Приращение независимой переменной D x в точке x 0 часто называют дифференциалом независимой переменной и обозначают символом dx. Таким образом, мы приходим к формуле
dy = dy (x 0) = f¢ (x 0)× dx. (5.5)
Из формулы (5.5) следует, что производную функции можно найти как частное дифференциалов:
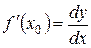 (5.6)
(5.6)
g Если функция y = f (x) дифференцируема в точке x 0, то в данной точке она непрерывна.
4 Пусть функция y = f (x) дифференцируема в точке x 0, то есть ее приращение в этой точке можно представить в виде (5.4). Переходя в равенстве (5.4) к пределу при D x ® 0, получим 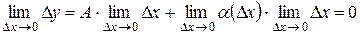 . В соответствие с первым определением непрерывности (см. §4.5), функция y = f (x) непрерывна в точке x 0. 3
. В соответствие с первым определением непрерывности (см. §4.5), функция y = f (x) непрерывна в точке x 0. 3
Обратное утверждение неверно. Например, функция y = | x | непрерывна во всех точках числовой оси (в том числе, в точке x 0 = 0). Однако данная функция не является дифференцируемой в точке x 0 = 0. Непосредственную проверку предоставляем читателям.
2. Применение дифференциала для приближенных вычислений. Геометрический смысл дифференциала.
Во многих задачах, не требующих повышенной точности, дифференциал можно использовать для приближенного вычисления значений функции. Предположим, что на некотором интервале (a, b) определена и непрерывна некоторая функция y = f (x). Пусть в некоторой точке x 0 Î(a, b) функция y = f (x) является дифференцируемой и пусть нам известно значение функции y 0 = f (x 0). Требуется найти значение функции y 1 = f (x 1) в точке x 1 Î (a, b), достаточно близкой к точке x 0.
Обозначим через D x = x 1 – x 0 приращение аргумента функции в точке x 0. Искомое значение функции y 1 можно найти приближенно, заменив приращение функции дифференциалом: y 1 = y 0 + D y» f (x 0) + dy (x 0). Таким образом, мы приходим к следующей приближенной формуле:
 f (x 1)» f (x 0) + f¢ (x 0)×(x 1 – x 0) (5.7)
f (x 1)» f (x 0) + f¢ (x 0)×(x 1 – x 0) (5.7)
Формула (5.7) имеет простой геометрический смысл. Из рисунка 5.2 видно, что если точка x 1 достаточно близка к точке x 0 то приращение функции y = f (x) можно приближенно заменить приращением касательной, проведенной к графику функции в точке А (x 0, y 0). Приращение касательной (отрезок ВС) легко находится из прямоугольного треугольника АВС:
ВС = АС×tga = f¢ (x 0)×D x = dy (x 0).
Таким образом, дифференциал функции в точке x 0 равен приращению касательной, проведенной к графику функции в точке
А (x 0, f (x 0)).
Пример 5.1. Вычислить 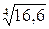 приближенно, с помощью дифференциала.
приближенно, с помощью дифференциала.
Рассмотрим функцию 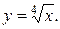
Пусть 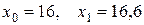 . Тогда
. Тогда 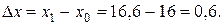
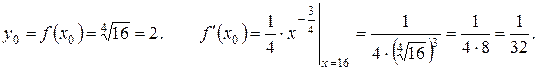
Для нахождения 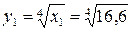 воспользуемся формулой (5.7).
воспользуемся формулой (5.7).
Получим 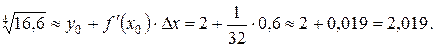
 2015-04-01
2015-04-01 1905
1905
