В ПИ-регуляторе только постоянная дифференцирования равна нулю, 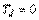 :
:
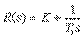
АЧХ ПИ-регулятора можно получить из рис. 5.36, если отбросить правую ветвь АЧХ с наклоном +20 дБ/дек. При этом сдвиг фаз на частотах выше 1 Гц (на рис. 5.36) не превысит уровень 0˚. Таким образом, ПИ-регулятор имеет два существенных положительных отличия от И-регулятора: во-первых, его усиление на всех частотах не может стать меньше 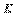 , следовательно, увеличивается динамическая точность регулирования, во-вторых, по сравнению с И-регулятором, он вносит дополнительный сдвиг фаз только в области низких частот, что увеличивает запас устойчивости замкнутой системы. Оба фактора дают дополнительные степени свободы для оптимизации качества регулирования. В то же время, как и в И-регуляторе, модуль коэффициента передачи регулятора с уменьшением частоты стремится к бесконечности, обеспечивая тем самым нулевую ошибку в установившемся режиме. Отсутствие сдвига фаз на высоких частотах позволяет увеличить скорость нарастания управляемой переменной (по сравнению с И-регулятором) без снижения запаса устойчивости. Однако это справедливо до тех пор, пока пропорциональный коэффициент
, следовательно, увеличивается динамическая точность регулирования, во-вторых, по сравнению с И-регулятором, он вносит дополнительный сдвиг фаз только в области низких частот, что увеличивает запас устойчивости замкнутой системы. Оба фактора дают дополнительные степени свободы для оптимизации качества регулирования. В то же время, как и в И-регуляторе, модуль коэффициента передачи регулятора с уменьшением частоты стремится к бесконечности, обеспечивая тем самым нулевую ошибку в установившемся режиме. Отсутствие сдвига фаз на высоких частотах позволяет увеличить скорость нарастания управляемой переменной (по сравнению с И-регулятором) без снижения запаса устойчивости. Однако это справедливо до тех пор, пока пропорциональный коэффициент 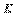 не станет настолько большой, что увеличит усиление контура до единицы на частоте
не станет настолько большой, что увеличит усиление контура до единицы на частоте  .
.
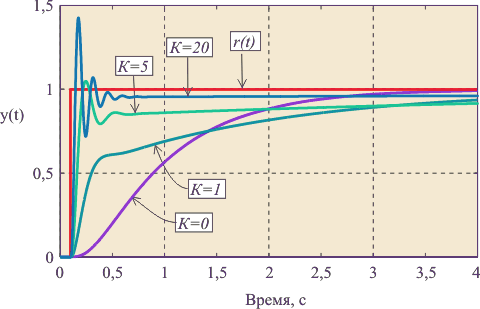
Рис. 5.39. Реакция замкнутой системы с ПИ регулятором на скачок 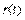 при
при 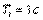 для объекта вида (5.50) при
для объекта вида (5.50) при 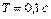
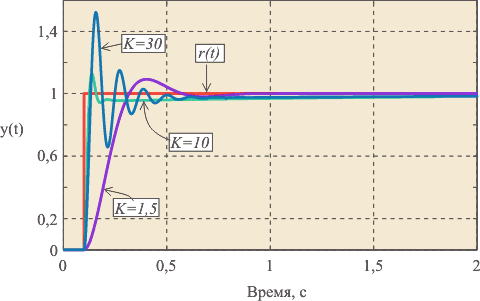
Рис. 5.40. Реакция замкнутой системы с ПИ регулятором на скачок 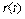 при
при 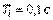 для объекта вида (5.50) при
для объекта вида (5.50) при 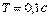
Переходный процесс в ПИ-регуляторе при разных сочетаниях 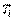 и
и 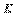 показан на рис. 5.39, рис. 5.40. При
показан на рис. 5.39, рис. 5.40. При 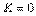 (рис. 5.39) получаем И-регулятор. С ростом пропорционального коэффициента
(рис. 5.39) получаем И-регулятор. С ростом пропорционального коэффициента 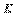 появляется дополнительная ошибка во время переходного процесса (см. также рис. 5.37 и (5.45)), которая уменьшается с ростом
появляется дополнительная ошибка во время переходного процесса (см. также рис. 5.37 и (5.45)), которая уменьшается с ростом 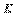 , однако при этом снижается запас устойчивости системы, поскольку с ростом
, однако при этом снижается запас устойчивости системы, поскольку с ростом 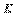 увеличивается усиление на частоте
увеличивается усиление на частоте 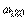 . Это приводит к появлению затухающих колебаний в начале переходного процесса (рис. 5.39). Когда величина
. Это приводит к появлению затухающих колебаний в начале переходного процесса (рис. 5.39). Когда величина 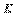 становится достаточно большой для компенсации ослабления сигнала в объекте на частоте
становится достаточно большой для компенсации ослабления сигнала в объекте на частоте 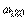 , в системе появляются незатухающие колебания.
, в системе появляются незатухающие колебания.
Следует отметить, что в отличие от П-регулятора, в котором ошибка остается в установившемся режиме, наличие интегрального члена в ПИ-регуляторе сводит эту ошибку в идеальном регуляторе до нуля, как в И-регуляторе. Выражение для ошибки ПИ-регулятора можно получить, подставив (5.51) в (5.41) и вычтя из полученного выражения 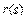 :
:
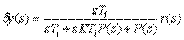 . . |
Как видим, при 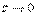 , т.е. в установившемся режиме, ошибка
, т.е. в установившемся режиме, ошибка 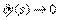 .
.
Однако появление пропорционального коэффициента приводит к затягиванию переходного процесса по сравнению с И-регулятором при тех же 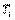 и
и 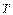 , (рис. 5.39). Объясняется это тем, что в ПИ-регуляторе сигнал ошибки
, (рис. 5.39). Объясняется это тем, что в ПИ-регуляторе сигнал ошибки 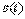 , поступающий на вход интегратора, меньше, чем в И-регуляторе (он уменьшается благодаря пропорциональному коэффициенту), поэтому сигнал, компенсирующий ошибку
, поступающий на вход интегратора, меньше, чем в И-регуляторе (он уменьшается благодаря пропорциональному коэффициенту), поэтому сигнал, компенсирующий ошибку 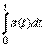 нарастает медленнее, чем в И-регуляторе. В частотной области этот процесс можно объяснить тем, что с ростом
нарастает медленнее, чем в И-регуляторе. В частотной области этот процесс можно объяснить тем, что с ростом 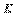 полюс
полюс 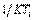 передаточной функции смещается влево (рис. 5.36), т.е. расширяется область частот, в которой интегральной составляющая пренебрежимо мала и ПИ-регулятор вырождается в чистый П-регулятор, для которого характерна статическая ошибка. В АЧХ замкнутой системы с большим
передаточной функции смещается влево (рис. 5.36), т.е. расширяется область частот, в которой интегральной составляющая пренебрежимо мала и ПИ-регулятор вырождается в чистый П-регулятор, для которого характерна статическая ошибка. В АЧХ замкнутой системы с большим 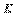 (рис. 5.41) появляется погрешность (уменьшение амплитуды выходного сигнала) в диапазоне частот выше
(рис. 5.41) появляется погрешность (уменьшение амплитуды выходного сигнала) в диапазоне частот выше 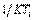 . С ростом
. С ростом 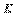 эта частота сдвигается влево, что во временной области соответствует затягиванию процесса установления.
эта частота сдвигается влево, что во временной области соответствует затягиванию процесса установления.
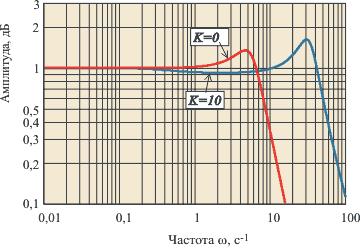
Рис. 5.41. АЧХ замкнутого контура с ПИ-регулятором при 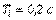 для объекта вида (5.50) при
для объекта вида (5.50) при 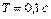
 2015-04-17
2015-04-17 1717
1717








