Задача 11.1 Изпартии в 5 изделий, среди которых одно бракованное, выбирают 2 изделия. Определить вероятность того, что среди двух изделий есть бракованное.
Решение. Обозначим через А событие - среди двух выбранных изделий, есть бракованное. Всего можно составить столько различных пар изделий, сколько может быть составлено сочетаний из пяти изделий по два, т.е. 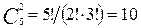 . Таким образом, общее число возможных элементарных исходов равно 10. Слова «выбор наугад» гарантируют равновозможность исходов. Благоприятствует событию А четыре исхода. Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:
. Таким образом, общее число возможных элементарных исходов равно 10. Слова «выбор наугад» гарантируют равновозможность исходов. Благоприятствует событию А четыре исхода. Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:
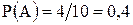 .
.
Задача 11.2. Ребёнок играет с шестью буквами азбуки: А, А, Е, К, Р, Т. Найти вероятность того, что он сможет сложить случайно слово «КАРЕТА».
Решение. Пусть событие А – получение слова «КАРЕТА». Различные комбинации шести букв из имеющихся шести представляют собой перестановки, так как отличаются только порядком следования букв; то есть общее число равновозможных элементарных исходов 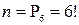 . Благоприятствуют событию А два исхода, так как перестановка двух букв А (
. Благоприятствуют событию А два исхода, так как перестановка двух букв А (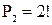 способами) не меняет собранное из карточек слово «КАРЕТА». Итак,
способами) не меняет собранное из карточек слово «КАРЕТА». Итак,
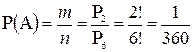 .
.
Задача 11.3. Группа из 5 женщин и 20 мужчин выбирает трёх делегатов. Считая, что каждый из присутствующих с одинаковой вероятностью может быть выбран, найти вероятность того, что выберут двух женщин и одного мужчину.
Решение. Общее число равновозможных элементарных исходов испытания равно числу способов, которыми можно выбрать трёх делегатов из 25 человек, то есть 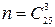 .
.
Определим число исходов, благоприятствующих интересующему нас событию А (выберут двух женщин и одного мужчину). Мужчина-делегат может быть выбран 20 способами. При этом остальные два делегата должны быть женщинами, а выбрать двух женщин из пяти можно 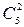 . Следовательно,
. Следовательно, 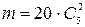 . Поэтому
. Поэтому
Р(А)= 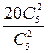 =
= 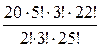 =
= 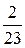 .
.
§11.3. Статистическая вероятность
Статистическое определение вероятности используется в случае, когда результаты испытания не являются равновозможными.
Относительная частота события А определяется равенством:
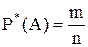 ,
,
где m – число испытаний, в которых событие А наступило, n – общее число произведенных испытаний.
Я. Бернулли доказал, что при неограниченном увеличении числа опытов относительная частота появления события имеет пределом некоторое постоянное число. Это постоянное число и есть вероятность появления события. Поэтому, естественно, относительную частоту появления события при достаточно большом числе испытаний называть статистической вероятностью в отличие от ранее введенной вероятности.
Пример 11.8. Как приближенно установить число рыб в озере?
Пусть в озере х рыб. Забрасываем сеть и, допустим, находим в ней n рыб. Каждую из них метим и выпускаем обратно. Через несколько дней в такую же погоду и в том же месте забрасываем ту же самую сеть и так повторяем несколько раз. Допустим, что находим в ней m рыб, среди которых k меченных. Пусть событие А – "пойманная рыба мечена". Тогда по определению относительной частоты
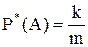 .
.
Но если в озере х рыб и мы в него выпустили n меченых, то
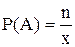 .
.
Так как
Р*(А)» Р(А), то 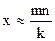 .
.
§11.4. Операции над событиями. Теорема сложения вероятностей
Суммой, или объединением, нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий (в одном и том же испытании).
Сумма А1 + А2 + … + Аn обозначается так:
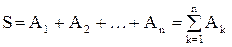 или
или 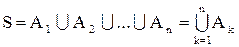 .
.
Пример 11.9. Бросаются две игральные кости. Пусть событие А состоит в выпадении 4 очков на 1 кости, а событие В – в выпадении 5 очков на другой кости. События А и В совместны. Поэтому событие А + В состоит в выпадении 4 очков на первой кости, или 5 очков на второй кости, или 4 очков на первой кости и 5 очков на второй одновременно.
Пример 11.10. Событие А – выигрыш по I займу, событие В – выигрыш по II займу. Тогда событие А + В – выигрыш хотя бы по одному займу (возможно по двум сразу).
Произведением или пересечением нескольких событий называется событие, состоящее в совместном появлении всех этих событий (в одном и том же испытании).
Произведение В событий А1, А2, …, Аn обозначается так:
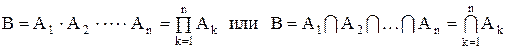 .
.
Пример 11.11. События А и В состоят в успешном прохождении I и II экзаменов соответственно при поступлении в институт. Тогда событие А×В состоит в успешном прохождении обоих экзаменов.
Понятия суммы и произведения событий имеют наглядную геометрическую интерпретацию. Пусть событие А есть попадание точки в область А, а событие В – попадание точки в область В. Тогда событие А + В есть попадание точки в объединение этих областей (рис. 11.1), а событие А × В есть попадание точки в пересечение этих областей (рис. 11.2).
 |
Рис. 11.1 Рис.11.2
1 Если события Ai (i = 1, 2, …, n) попарно несовместны, то вероятность суммы событий равна сумме вероятностей этих событий:
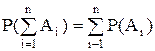 .
.
Пусть А и Ā – противоположные события, т.е. А + Ā = W, где W - достоверное событие. Из теоремы сложения вытекает, что
Р(W) = Р(А) + Р(Ā) = 1,
поэтому
Р(Ā) = 1 - Р(А).
Если события А1 и А2 совместны, то вероятность суммы двух совместных событий равна:
Р(А1 + А2) = Р(А1) + Р(А2) – Р(А1×А2).
Теоремы сложения вероятностей позволяют перейти от непосредственного подсчета вероятностей к определению вероятностей наступления сложных событий.
Задача 11.4. Стрелок производит один выстрел по мишени. Вероятность выбить 10 очков (событие А), 9 очков (событие В) и 8 очков (событие С) равны соответственно 0,11; 0,23; 0,17. Найти вероятность того, что при одном выстреле стрелок выбьет менее 8 очков (событие D).
Решение. Перейдем к противоположному событию 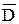 – при одном выстреле стрелок выбьет не менее 8 очков. Событие
– при одном выстреле стрелок выбьет не менее 8 очков. Событие 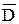 наступает, если произойдет А или В, или С, т.е.
наступает, если произойдет А или В, или С, т.е. 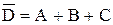 . Так как события А, В, С попарно несовместны, то, по теореме сложения,
. Так как события А, В, С попарно несовместны, то, по теореме сложения,
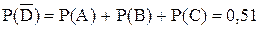 .
.
Откуда
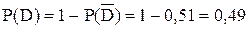 .
.
Задача 11.5. От коллектива бригады, которая состоит из 6 мужчин и 4 женщин, на профсоюзную конференцию выбирается два человека. Какова вероятность, что среди выбранных хотя бы одна женщина (событие А).
Решение. Если произойдет событие А, то обязательно произойдет одно из следующих несовместных событий: В – "выбраны мужчина и женщина"; С – "выбраны две женщины". Поэтому можно записать: А = В + С. Найдем вероятность событий В и С. Два человека из 10 можно выбрать 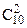 способами. Двух женщин из 4 можно выбрать
способами. Двух женщин из 4 можно выбрать 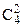 способами. Мужчину и женщину можно выбрать 6×4 способами. Тогда
способами. Мужчину и женщину можно выбрать 6×4 способами. Тогда 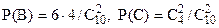 . Так как события В и С несовместны, то, по теореме сложения,
. Так как события В и С несовместны, то, по теореме сложения,
Р(А) = Р(В + С) = Р(В) + Р(С) = 8/15 + 2/15 = 2/3.
§11.5. Условная вероятность. Теорема умножения вероятностей
Условной вероятностью Р(В/А) называется вероятность события В, вычисленная в предположении, что событие А уже наступило.
Теорема. Вероятность совместного появления двух событий равна произведению вероятностей одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
Р(А×В) = Р(А)×Р(В/А). (11.1)
Два события называются независимыми, если появление любого из них не изменяет вероятность появления другого, т.е.
Р(А) = Р(А/В) или Р(В) = Р(В/А). (11.2)
Если события А и В независимы, то из формул (12.1) и (12.2) следует
Р(А×В) = Р(А) × Р(В). (11.3)
Справедливо и обратное утверждение, т.е. если для двух событий выполняется равенство (11.3), то эти события независимы. В самом деле, из формул (11.3) и (11.1) вытекает Р(А×В) = Р(А)×Р(В) = Р(А)× Р(В/А), откуда Р(А) = Р(В/А).
Формула (11.1) допускает обобщение на случай конечного числа событий А1, А2,…,Аn:
Р(А1 А2…Аn) = Р(А1) × Р(А2/А1) × Р(А3/А1А2) ×…×Р(Аn/А1А2…Аn-1).
Задача 11.6. Из урны, в которой 5 белых и 10 черных шаров, вынимают подряд два шара. Найти вероятность того, что оба шара белые (событие А).
Решение. Рассмотрим события: В – первый вынутый шар белый; С – второй вынутый шар белый. Тогда А = ВС.
Опыт можно провести двумя способами:
1) с возвращением: вынутый шар после фиксации цвета возвращается в урну. В этом случае события В и С независимы:
Р(А) = Р(В) × Р(С) = 5/15×5/15 = 1/9;
2) без возвращения: вынутый шар откладывается в сторону. В этом случае события В и С зависимы:
Р(А) = Р(В) × Р(С/В).
Для события В условия прежние, 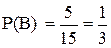 , а для С ситуация изменилась. Произошло В, следовательно в урне осталось 14 шаров, среди которых 4 белых.
, а для С ситуация изменилась. Произошло В, следовательно в урне осталось 14 шаров, среди которых 4 белых.
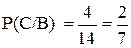 .
.
Итак,
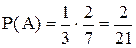 .
.
Задача 11.7. Среди 50 электрических лампочек 3 нестандартные. Найти вероятность того, что две взятые одновременно лампочки нестандартные.
Решение. Рассмотрим события: А – первая лампочка нестандартная, В – вторая лампочка нестандартная, С – обе лампочки нестандартные. Ясно, что С = А × В. Событию А благоприятствуют 3 случая из 50 возможных, т.е. Р(А) = 3/50. Если событие А уже наступило, то событию В благоприятствуют два случая из 49 возможных, т.е. Р(В/А) = 2/49. Следовательно,
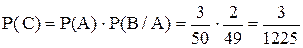 .
.
Задача 11.8. Два спортсмена независимо друг от друга стреляют по одной мишени. Вероятность попадания в мишень первого спортсмена равна 0,7, а второго – 0,8. Какова вероятность того, что мишень будет поражена?
Решение. Мишень будет поражена, если в нее попадет либо первый стрелок, либо второй, либо оба вместе, т.е. произойдет событие А + В, где событие А заключается в попадании в мишень первым спортсменом, а событие В – вторым. Тогда
Р(А+В) = Р(А) + Р(В) – Р(А × В) = 0,7 + 0,8 – 0,7 × 0,8 = 0,94.
§11.6. Формула полной вероятности и формула Байеса
Пусть Н1, Н2,…, Нn – попарно несовместные события, образующие полную группу (гипотезы), и А – событие, которое может произойти только совместно с одним из них
Пусть, кроме того, нам известны Р(Нi) и Р(А/Нi) (i = 1, 2, …, n).
В этих условиях справедливы формулы:
|
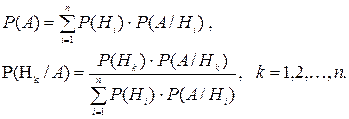
Формула (11.4) называется формулой полной вероятности. По ней вычисляется вероятность события А (полная вероятность).
Формула (11.5) называется формулой Байеса. Она позволяет произвести пересчет вероятностей гипотез, если событие А произошло.
Задача 11.9. В корзине яблоки с четырех деревьев одного сорта. С первого – 15% всех яблок, со второго – 35%, с третьего – 20%, с четвертого – 30%. Созревшие яблоки составляют соответственно 99%, 97%, 98%, 95%.
а) Какова вероятность того, что наугад взятое яблоко окажется спелым (событие А).
б) При условии, что наугад взятое яблоко оказалось спелым, вычислить вероятность того, что оно с первого дерева.
Решение. а) Имеем 4 гипотезы:
Н1 – наугад взятое яблоко снято с 1-го дерева;
Н2 – наугад взятое яблоко снято с 2-го дерева;
Н3 – наугад взятое яблоко снято с 3-го дерева;
Н4 – наугад взятое яблоко снято с 4-го дерева.
Их вероятности по условию: Р(Н1) = 0,15; Р(Н2) = 0,35; Р(Н3) = 0,2; Р(Н4) = 0,3.
Условные вероятности события А:
Р(А/Н1) = 0,99; Р(А/Н2) = 0,97; Р(А/Н3) = 0,98; Р(А/Н4) = 0,95.
Вероятность того, что наудачу взятое яблоко окажется спелым, находится по формуле полной вероятности:
Р(А) = Р(Н1) × Р(А/Н1) + Р(Н2) × Р(А/Н2) + Р(Н3) × Р(А/Н3) + Р(Н4) × Р(А/Н4) =
= 0, 969.
б) Формула Байеса для нашего случая имеет вид:
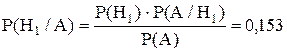 .
.
Глава 12. Случайные величины
§12.1. Определения, примеры
Часто в результате испытания происходят события, заключающиеся в том, что некоторая величина принимает одно из своих возможных значений.
В таких случаях удобно вместо множества событий рассматривать одну переменную величину (называемую случайной величиной). Случайная величина обозначается через X, Y, Z, … и т.д.
Случайной называется величина, которая в результате испытания может принять то или иное возможное значение, неизвестное заранее, но обязательно одно.
Пример 12.1. В студенческой группе 25 человек. Пусть величина Х – число студентов, находящихся в аудитории перед началом занятий. Ее возможными значениями будут числа 0, 1, 2,…,25.
При каждом испытании (начало занятий) величина Х обязательно примет одно из своих возможных значений, т.е. наступит одно из событий
Х = 0, Х = 1, …, Х = 25.
Пример 12.2. Измерение роста юношей призывного возраста. Возможные события заключаются в том, что рост Y примет некоторое значение в пределах от 140 до 230 см.
Пример 12.3. Однократное бросание игральной кости. Возможные события заключаются в том, что на верхней грани выпадает Z: 1, 2, 3, 4, 5, 6.
Пример 12.4. Подбрасывается монета n раз. Возможные результаты: герб выпал 0, 1, 2, …, n раз.
Различают дискретные и непрерывные случайные величины.
Если множество возможных значений случайной величины конечно или образуют бесконечную числовую последовательность, то такая случайная величина называется дискретной (примеры 12.1, 12.3, 12.4).
Случайная величина, множество значений которой заполняет сплошь некоторый числовой промежуток, называется непрерывной (пример 12.2). Заметим, что дискретные и непрерывные величины не исчерпывают все типы случайных величин.
Если случайная величина не относится ни к дискретным, ни к непрерывным случайным величинам, то ее называют смешанной.
Очевидно, что для полной характеристики дискретной случайной величины мало знать ее значения. Необходимо им поставить в соответствие вероятности.
Соответствие между всеми возможными значениями дискретной случайной величины и их вероятностями называется законом распределения данной случайной величины.
Простейшая формой задания закона распределения дискретной случайной величины является таблица, в которой перечислены возможные значения случайной величины (обычно в порядке возрастания) и соответствующие им вероятности:
| Х | х1 | х2 | … | хn | … |
| Р | р1 | р2 | … | рn | … |
Такая таблица называется рядом распределения. Допустим, что число возможных значений случайной величины конечно: х1, х2, …, хn. При одном испытании случайная величина принимает одно и только одно постоянное значение. Поэтому события Х = хi (i = 1, 2, …, n) образуют полную группу попарно несовместных событий. Следовательно, р1 + р2 + … + рn = 1.
Можно закон распределения изобразить и графически, откладывая на оси абсцисс возможные значения случайной величины, а на оси ординат – соответствующие вероятности. Для большей выразительности полученные точки соединяются прямолинейными отрезками. Получающая при этом фигура называется многоугольником (полигоном) распределения.
§12.2. Функция распределения вероятностей
Непрерывную случайную величину нельзя охарактеризовать перечнем всех возможных ее значений и их вероятностей. Естественно, встает вопрос о том, нельзя ли охарактеризовать случайную величину иным способом, одинаково годным как для дискретных, так и для непрерывных случайных величин.
Функцией распределения случайной величины Х называют функцию F(x), определяющую для каждого значения х, вероятность того, что случайная величина Х примет значение меньше х, т.е.
F(x) = P(X<x).
Иногда функцию F(x) называют интегральной функцией распределения.
Функция распределения обладает следующими свойствами:
1. Значение функции распределения принадлежит отрезку [0,1]:
0£F(x)£ 1.
2. Функции распределения есть неубывающая функция.
3. Вероятность того, что случайная величина Х примет значение, заключенное в интервале (а, b), равна приращению функции распределения на этом интервале:
Р(а < X < b) = F(b) – F(а). (12.1)
Если все возможные значения случайной величины Х принадлежат интервалу (а, b), то
F(x) = 0 при х£ а; F(x) = 1 при х³b.
4. Справедливы следующие предельные отношения:

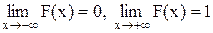 .
.
Для дискретной случайной величины Х, которая может принимать значения х1, х2, …,хn, функция распределения имеет вид
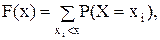
где неравенство под знаком суммы означает, что суммирование касается всех тех значений хi, величина которых меньше х.
Поясним эту формулу исходя из определения функции F(x). Предположим, что аргумент х принял какое-то определенное, но такое, что выполняется неравенство xi<x£xi+1. Тогда левее числа х на числовой оси окажутся только те значения случайной величины, которые имеют индекс 1, 2, 3, …, i. Поэтому неравенство Х<x выполняется, если величина Х примет значения хк, где
к = 1, 2, …, i. Таким образом, событие Х<x наступит, если наступит любое, неважно какое, из событий Х = х1, Х = х2, Х = х3, …, Х = хi. Так как эти события несовместны, то по теореме сложения вероятностей имеем
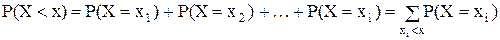 . (12.2)
. (12.2)
Предположим теперь, что для непрерывной случайной величины Х ее функция распределения F(x) имеет непрерывную производную
F'(x) = j(x).
Функцию j(x) называют плотностью вероятности (для данного распределения) или дифференциальной функцией распределения.
Так как плотность вероятности j(x) является производной неубывающей функции F(x), то она неотрицательна: j(x)³0. В отличие от функции распределения, плотность вероятности может принимать сколь угодно большие значения.
Так как F(x) является первообразной для j(x), то на основании формулы Ньютона-Лейбница имеем
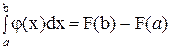 .
.
Отсюда в силу (12.1) получаем
P(a £ X £ b) = 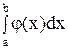 . (12.3)
. (12.3)
Полагая а = -¥ и b = +¥, получаем достоверное событие Х Î (-¥, +¥), вероятность которого равна единице. Следовательно,
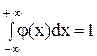 .
.
В частности, если все возможные значения случайной величины принадлежат интервалу (а, b), то
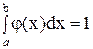 .
.
Полагая в формуле а = -¥, b = х и обозначая для ясности переменную интегрирования t, получим функцию распределения
F(x) = P(-¥ < X < x) = 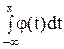 .
.
Задача 12.1. Найти интегральную функцию распределения случайной величины Х, заданной рядом распределения:
| Х | |||
| Р | 0,3 | 0,2 | 0,5 |
и построить ее график.
Решение. Пусть х £ 1, тогда F(x) = 0, так как событие Х < х будет невозможным. Если 1< х £ 2, то на основании равенства (12.2) имеем F(x) = p1 = 0,3. Если 2< х £ 3, то F(x) = p1 + p2 = 0,5. Если х > 3, то F(x) = p1 + p2 + p3 = 1. Окончательно получаем
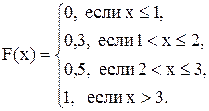
График функции F(х) изображен на рис. 12.1.
 F(х)
F(х)


 1
1


 0,5
0,5


 0,3
0,3


0 1 2 3 х
Рис.12.1
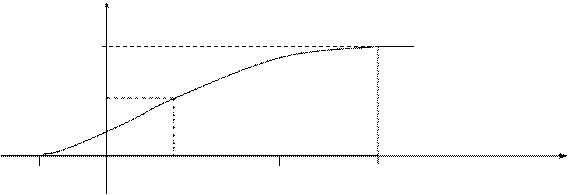
Задача 12.2. Функция распределения случайной величины Х задана выражением
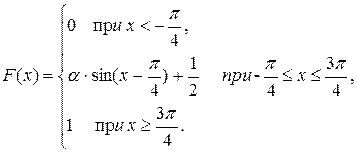
Найти коэффициент a; вероятность попадания значения случайной величины Х в результате опыта в интервал (p/4; 3p/4); построить график функции.
Решение. При х = 3p/4 функция F(x) равна 1, т.е.
a×sin (3p/4 - p/4) +1/2 = 1
или
a×sin (p/2) + 1/2 = 1,
откуда a = 1/2.
Подставляя а = p/4 и b = 3p/4 в равенство (12.1), получаем
Р(p/4 < X <3p/4) = F(3p/4) - F(p/4) = 1 - 1/2 × sin0 - 1/2 = 1/2.
График функции у =1/2×sin(х-p/4)+1/2 отличается от графика функции у = sinх тем, что он "сжат" по оси Оу в два раза, сдвинут вправо на p/4, поднят вверх на 1/2. Воспользовавшись этим замечанием, отразим график F(x) (рис. 12.2).
 F(x)
F(x)
 | |||
 |
- p/4 0 p/4 p/2 3p/4 x
Рис. 12.2
Задача 12.3. Средняя продолжительность жизни определенного типа радиоламп (в часах) имеет следующую плотность распределения:
j(х)= 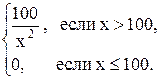
Вычислить:
а) вероятность того, что лампа не будет заменена в первые 150 часов функционирования;
б) вероятность того, что лампа будет функционировать более 200 часов и в то же время менее 300 часов.
Решение. а) Обозначим время функционирования лампы через Х. Мы знаем, что Р(Х > 150) = 1 – Р(Х < 150) и что Р(Х < 150) = F(150). В то же время
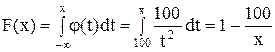 .
.
Следовательно, Р(Х > 150) = 1 – 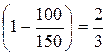 .
.
б) 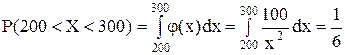 .
.
§12.3. Числовые характеристики случайной величины
Функция распределения содержит полную информацию о случайной величине. На практике функцию распределения не всегда можно установить; иногда такого исчерпывающего знания и не требуется. Частичную информацию о случайной величине дают числовые характеристики, которые в зависимости от рода информации делятся на следующие группы.
1. Характеристики положения случайной величины на числовой оси (мода Мo, медиана Мe, математическое ожидание М(Х)).
2. Характеристики разброса случайной величины около среднего значения (дисперсия D(X), среднее квадратическое отклонение s (х)).
3. Характеристики формы кривой y = j(x) (асимметрия As, эксцесс Ех).
Рассмотрим подробнее каждую из указанных характеристик.
Математическое ожидание случайной величины Х указывает некоторое среднее значение, около которого группируются все возможные значения Х. Для дискретной случайной величины, которая может принимать лишь конечное число возможных значений, математическим ожиданием называют сумму произведений всех возможных значений случайной величины на вероятность этих значений:
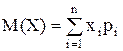 . (12.4)
. (12.4)
Для непрерывной случайной величины Х, имеющей заданную плотность распределения j(x) математическим ожиданием называется следующий интеграл:
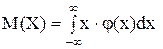 . (12.5)
. (12.5)
Здесь предполагается, что несобственный интеграл 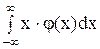 cходится абсолютно. Свойства математического ожидания:
cходится абсолютно. Свойства математического ожидания:
1. М(С) = C, где С = const;
2. M(C × Х) = С × М(Х);
3. М(Х ± Y) = М(Х) ± М(Y), где X и Y – любые случайные величины;
4. М(Х ×Y) = М(Х) × М(Y), где X и Y – независимые случайные величины.
Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина.
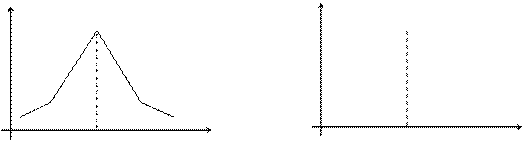
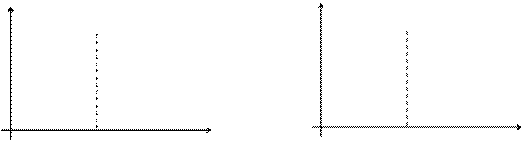
Модой дискретной случайной величины, обозначаемой Мо, называется ее наиболее вероятное значение (рис.12.3), а модой непрерывной случайной величины – значение, при котором плотность вероятности максимальна (рис. 12.4).

 Р j(x)
Р j(x)
0 Мо x 0 Мо x
Рис. 12.3 Рис.12.4
Медианой непрерывной случайной величины Х называется такое ее значение Ме, для которого одинаково вероятно, окажется ли случайная величина меньше или больше Ме, т.е.
Р(Х < Ме) = Р(X > Ме)
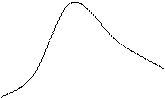
Из определения медианы следует, что Р(Х < Ме) = 0,5, т.е. F(Ме) = 0,5. Геометрически медиану можно истолковывать как абсциссу, в которой ордината j(x) делит пополам площадь, ограниченную кривой распределения (рис. 12.5). В случае симметричного распределения медиана совпадает с модой и математическим ожиданием (рис. 12.6).
 j(x) j(x)
j(x) j(x)
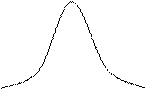 |
0 Ме x 0 Мо =Ме =М(Х) x
Рис. 12.5 Рис. 12.6
Дисперсией случайной величины называется математическое ожидание квадрата ее отклонения от математического ожидания
D(X) = M(X –М(Х))2.
Дисперсию случайной величины Х удобно вычислять по формуле:
а) для дискретной величины
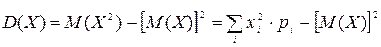 ; (12.6)
; (12.6)
б) для непрерывной случайной величины
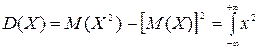 j(х)dx – [M(X)]2 (12.7)
j(х)dx – [M(X)]2 (12.7)
Дисперсия обладает следующими свойствами:
1. D(C) = 0, где С = const;
2. D(C×X) = C2×D(X);
3. D(X±Y) = D(X) + D(Y), если X и Y независимые случайные величины.
Средним квадратическим отклонением случайной величины Х называется арифметический корень из дисперсии, т.е. s(X) = 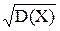 .
.
Заметим, что размерность s(х) совпадает с размерностью самой случайной величины Х, поэтому среднее квадратическое отклонение более удобно для характеристики рассеяния.
Обобщением основных числовых характеристик случайных величин является понятие моментов случайной величины.
Начальным моментом k-го порядка ak случайной величины Х называется математическое ожидание величины Хk, т.е. ak = М(Хk).
Начальный момент первого порядка – это математическое ожидание случайной величины.
Центральным моментом k-го порядка mk случайной величины Х называется математическое ожидание величины (Х-М(Х))k, т.е. mk= М(Х- -М(Х))k.
Центральный момент второго порядка это дисперсия случайной величины.
Для дискретной случайной величины начальный момент выражается суммой ak = 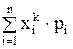 , а центральный – суммой mk =
, а центральный – суммой mk = 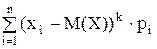 , где рi=p(X=xi). Для начального и центрального моментов непрерывной случайной величины можно получить следующие равенства:
, где рi=p(X=xi). Для начального и центрального моментов непрерывной случайной величины можно получить следующие равенства:
ak = 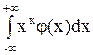 ,
,
mk = 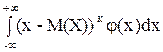 ,
,
где j(x) – плотность распределения случайной величины Х.
Величина 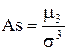 называется коэффициентом асимметрии.
называется коэффициентом асимметрии.
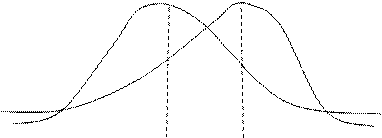
Если коэффициент асимметрии отрицательный, то это говорит о большом влиянии на величину m3 отрицательных отклонений. В этом случае кривая распределения (рис.12.7) более полога слева от М(Х). Если коэффициент As положительный, а значит, преобладает влияние положительных отклонений, то кривая распределения (рис.12.7) более полога справа. Практически определяют знак асимметрии по расположению кривой распределения относительно моды (точки максимума дифференциальной функции).
 |
 j(x)
j(x)
As>0 As<0

0 М(Х) М(Х) x
Рис. 12.7
Эксцессом Ех называется величина
Ех = m4/s4 – 3.
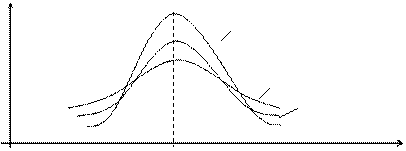
Можно показать, что для наиболее распространенного в природе нормального закона распределения, который будет рассматриваться в следующем параграфе, отношение m4/s4 = 3. Поэтому эксцесс служит для сравнения данного распределения с нормальным, у которого эксцесс равен нулю. Можно было бы доказать, что распределения более островершинные, чем нормальное, имеют эксцесс Ех > 0, а более плосковершинные – имеют эксцесс Ех < 0 (рис.12.8).
 j(x)
j(x)
 Ех>0
Ех>0
Ex<0
Ex=0 (кривая нормального
распределения)
0 х
Рис. 12.8
Задача 12.4. Дискретная случайная величина Х задана законом распределения:
| Х | ||||
| р | 0,4 | 0,1 | 0,3 | 0,2 |
Найти математическое ожидание, дисперсию, среднее квадратическое отклонение.
Решение. Так как случайная величина является дискретной, то для вычисления М(Х) воспользуемся формулой (12.4). Имеем
М(х) = х1 × р1 + х2 × р2 + х3 × р3 + х4 × р4 = 0×0,4 + 1×0,1 + 2×0,3 + 3×0,2 = 1,3.
Найдем дисперсию D(x). Предварительно найдем математическое ожидание от х2:
М(х2) = х12 × р1 + х22× р2 + х32× р3 + х42× р4 = 02×0,4 + 12×0,1 + 22×0,3 + 32×0,2 = 3,1.
Далее по формуле (12.6) получаем
D(X) = 3,1 –1,32 = 3,1 – 1,69 = 1,41.
Найдем среднее квадратическое отклонение. Имеем
s(х) = 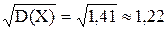 .
.
Задача 12.5. Непрерывная случайная величина Х задана функцией распределения
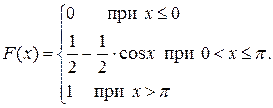
Найти математическое ожидание и дисперсию этой случайной величины.
Решение. По определению дифференциальной функции j(х) = F¢(x). Отсюда
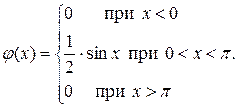
В точках х = 0 и х = p функция j(х) не дифференцируема. По формуле (12.5) получаем
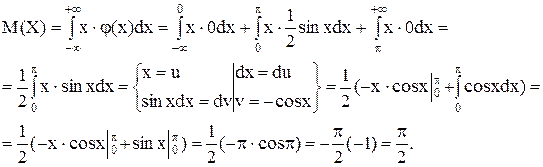
Находим сначала М(Х2). Имеем
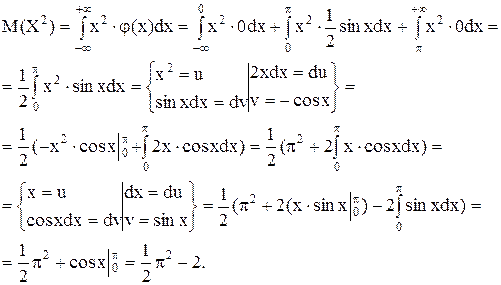
Далее по формуле (12.7) получаем
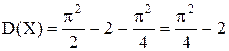 .
.
Задача 12.6. Случайная величина задана функцией
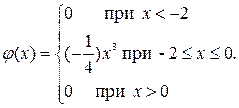
Найти коэффициент асимметрии и эксцесс.
Решение. Предварительно вычислим начальные моменты до четвертого порядка. Имеем:
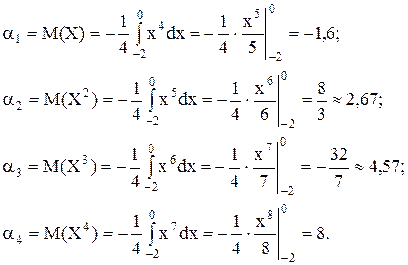
Теперь, воспользовавшись следующими формулами (они легко получаются из определения и свойств математического ожидания и дисперсии), найдем центральные моменты:
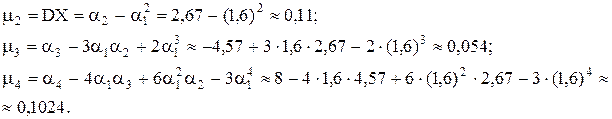
Отсюда следует, что
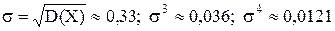 .
.
Далее имеем
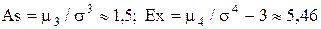 .
.
§12.4. Теоретические распределения
 2015-04-01
2015-04-01 9785
9785
