В общем случае дифференциальное уравнение первого порядка имеет вид:
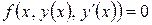 (10.2)
(10.2)
2 Задача нахождения частного решения дифференциального уравнения (10.2), удовлетворяющего некоторому начальному условию, называют задачей Коши:
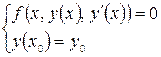 (10.3)
(10.3)
Рассмотрим некоторые типы дифференциальных уравнений первого порядка.
1. Дифференциальные уравнения с разделяющимися переменными
2 Дифференциальными уравнениями с разделяющимися переменными называются уравнения вида
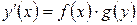 . (10.4)
. (10.4)
Общее решение дифференциальных уравнений с разделяющимися переменными находят с помощью метода, который так и называется «метод разделения переменных»:
1. В уравнении (10.4) производную 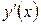 представим, как частное дифференциалов
представим, как частное дифференциалов 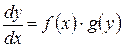 .
.
2. Умножим обе части полученного уравнения на dx и разделим на g(y):
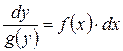 (переменные разделились).
(переменные разделились).
3. Интегрируя обе части полученного уравнения, находим общий интеграл исходного дифференциального уравнения 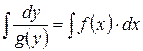 .
.
Замечание. Если 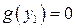 , то
, то 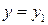 также будет интегралом уравнения (10.4), который может быть потерян при разделении переменных. В дальнейшем исследование таких интегралов опускается.
также будет интегралом уравнения (10.4), который может быть потерян при разделении переменных. В дальнейшем исследование таких интегралов опускается.
Пример 10.2. Найти общее решение дифференциального уравнения: 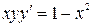 .
.
Очевидно, что данное уравнение является уравнением с разделяющимися переменными. Разделяя переменные, получим:
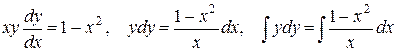 .
.
Таким образом, мы находим общий интеграл дифференциального уравнения: 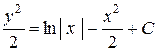 , или
, или 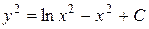 .
.
Замечание. Если 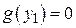 , то y = y 1 также будет интегралом (решением) уравнения (10.4), который может быть потерян при разделении переменных. В дальнейшем исследование таких интегралов опускается.
, то y = y 1 также будет интегралом (решением) уравнения (10.4), который может быть потерян при разделении переменных. В дальнейшем исследование таких интегралов опускается.
2. Однородные дифференциальные уравнения 1-го порядка
2 Дифференциальные уравнения первого порядка 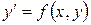 называются однородными, если
называются однородными, если 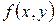 является однородной функцией. Т.е.
является однородной функцией. Т.е. 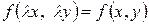 , для любого
, для любого 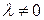 .
.
Если 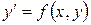 – однородное дифференциальное уравнение первого порядка, то оно с помощью замены
– однородное дифференциальное уравнение первого порядка, то оно с помощью замены 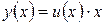 сводится к дифференциальному уравнению с разделяющимися переменными. При этом
сводится к дифференциальному уравнению с разделяющимися переменными. При этом 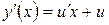 .
.
Задача 10.3. Решить задачу Коши:
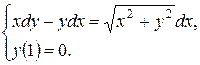
Решение. Преобразуем данное дифференциальное уравнение к виду 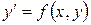 . Для этого разделим обе его части на dx:
. Для этого разделим обе его части на dx:
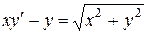 , или
, или 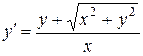 . Подставляя lx вместо x и ly вместо y в правую часть полученного уравнения, мы убеждаемся в том, что оно является однородным:
. Подставляя lx вместо x и ly вместо y в правую часть полученного уравнения, мы убеждаемся в том, что оно является однородным:
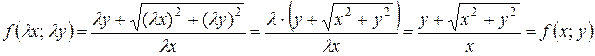 .
.
Произведем замену переменной 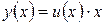 ,
, 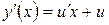 . При этом наше дифференциальное уравнение примет вид:
. При этом наше дифференциальное уравнение примет вид:
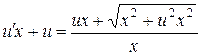 . Откуда
. Откуда 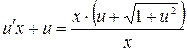 , или
, или 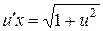 . Полученное дифференциальное уравнение является уравнением с разделяющимися переменными. Найдем его общее решение:
. Полученное дифференциальное уравнение является уравнением с разделяющимися переменными. Найдем его общее решение:
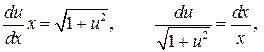
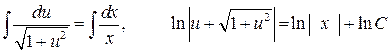 .
.
Откуда 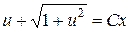 . Производя обратную замену
. Производя обратную замену 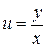 , мы получим общий интеграл исходного дифференциального уравнения:
, мы получим общий интеграл исходного дифференциального уравнения: 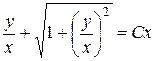 , или
, или 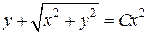 . Найдем такое значение константы С, при котором общий интеграл дифференциального уравнения удовлетворяет начальному условию
. Найдем такое значение константы С, при котором общий интеграл дифференциального уравнения удовлетворяет начальному условию 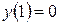 . Для этого подставим
. Для этого подставим 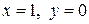 в общее решение:
в общее решение: 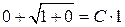 . Откуда
. Откуда 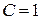 .
.
Подставляя найденную константу С в общий интеграл мы получим искомое решение исходной задачи Коши:
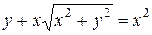 .
.
3. Линейные дифференциальные уравнения 1-го порядка
2 Дифференциальные уравнения вида
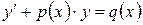 , (10.5)
, (10.5)
где 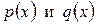 – функции, зависящие только от переменной x, называются линейными дифференциальными уравнениями первого порядка.
– функции, зависящие только от переменной x, называются линейными дифференциальными уравнениями первого порядка.
Линейные дифференциальные уравнения обычно решают при помощи замены переменных:
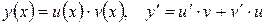 , (10.6)
, (10.6)
причем при такой замене, обе неизвестные функции находятся как решения дифференциальных уравнений с разделяющимися переменными.
Задача 10.4. Решить задачу Коши:
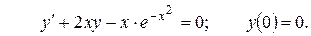
Решение. 1) Найдем общее решение дифференциального уравнения. Данное уравнение первого порядка является линейным. Следовательно, произведем следующую замену переменной:
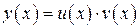 ,
, 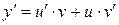 . Тогда
. Тогда
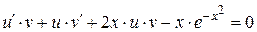 или
или 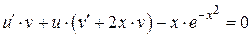 .
.
Подберем теперь такую функцию v (x), чтобы v ¢+2 xv =0. То есть v (x) будем искать как частное решение дифференциального уравнения с разделяющимися переменными:
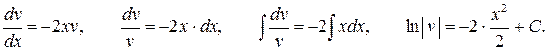
При С = 0 получим: ln| v | = – x 2. Следовательно, 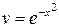 .
.
При таком выборе функции v (x) исходное дифференциальное уравнение примет вид: 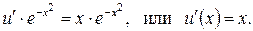
Следовательно, 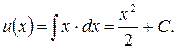 Таким образом,
Таким образом,
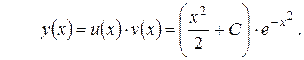
2) Для решения задачи Коши воспользуемся начальным условием y (0)=0.
Тогда 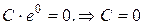 и, следовательно,
и, следовательно, 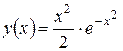 .
.
 2015-04-01
2015-04-01 792
792








