1. Дифференциальные уравнения вида 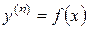 .
.
Уравнения вида 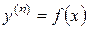 решаются при помощи n – кратного интегрирования. Рассмотрим пример.
решаются при помощи n – кратного интегрирования. Рассмотрим пример.
Пример 10.5. Найти общее решение дифференциального уравнения
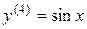 .
.
Четырежды проинтегрируем данное уравнение по переменной x:
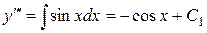 ,
,
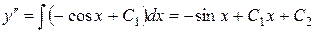 ,
,
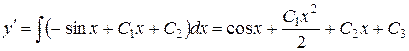 ,
,
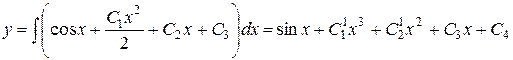 ,
,
где 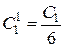 ,
, 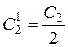 .
.
Таким образом, общее решение исходного уравнения четвертой степени 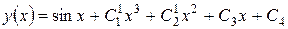 зависит от четырех произвольных констант.
зависит от четырех произвольных констант.
В дальнейшем мы ограничимся рассмотрением дифференциальных уравнений второго порядка 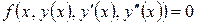 . Задача Коши для дифференциального уравнения второго порядка имеет вид:
. Задача Коши для дифференциального уравнения второго порядка имеет вид:
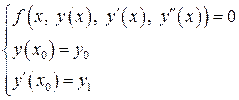 . (10.7)
. (10.7)
2. Дифференциальные уравнения вида 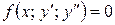 .
.
Если в дифференциальном уравнении второго порядка отсутствует переменная y, то с помощью замены переменной 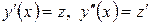 , данное уравнение сводится к дифференциальному уравнению первого порядка
, данное уравнение сводится к дифференциальному уравнению первого порядка 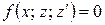 .
.
Пример 10.6. Найти общее решение дифференциального уравнения:
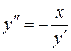 .
.
Произведем замену переменной: 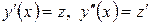 . Тогда мы получим дифференциальное уравнение первого порядка с разделяющимися переменными:
. Тогда мы получим дифференциальное уравнение первого порядка с разделяющимися переменными: 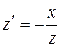 . Разделяя переменные, получим:
. Разделяя переменные, получим:
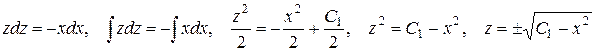 . Очевидно, что константа
. Очевидно, что константа 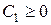 . При этом можно обозначить
. При этом можно обозначить 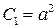 . Мы получили общее решение
. Мы получили общее решение 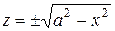 дифференциального уравнения
дифференциального уравнения 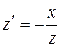 . Для того, чтобы найти общее решение исходного уравнения
. Для того, чтобы найти общее решение исходного уравнения 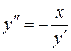 мы должны вспомнить, что
мы должны вспомнить, что 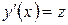 . Таким образом,
. Таким образом, 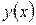 можно найти, решая дифференциальное уравнение
можно найти, решая дифференциальное уравнение 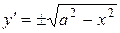 :
:
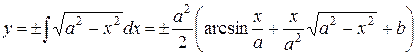 .
.
Читателям, в качестве упражнения, предлагаем найти данный интеграл самостоятельно.
В полученном общем решении 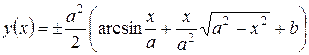 исходного дифференциального уравнения
исходного дифференциального уравнения 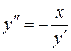 участвуют две произвольные константы a и b.
участвуют две произвольные константы a и b.
3. Дифференциальные уравнения вида 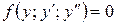 .
.
Если в дифференциальном уравнении второго порядка отсутствует переменная x, то с помощью замены переменной 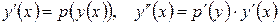 , (или просто
, (или просто 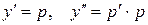 ) данное уравнение сводится к дифференциальному уравнению первого порядка
) данное уравнение сводится к дифференциальному уравнению первого порядка 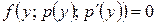 .
.
Пример 10.7. Найти общее решение дифференциального уравнения:
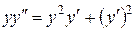 .
.
Произведем замену переменной: 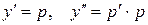 . Мы получим дифференциальное уравнение первого порядка относительно переменной y:
. Мы получим дифференциальное уравнение первого порядка относительно переменной y:
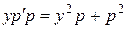 . После сокращения на p, мы убеждаемся в том, что данное уравнение
. После сокращения на p, мы убеждаемся в том, что данное уравнение 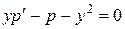 является линейным. Как обычно, его решение найдем, произведя замену
является линейным. Как обычно, его решение найдем, произведя замену 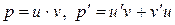 :
:
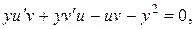
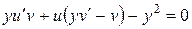 . (10.8)
. (10.8)
1) Подберем функцию v, предполагая, что 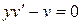 (при этом уравнение (10.8) становится существенно проще). Т.е. функция v (x) является произвольным частным решением дифференциального уравнения
(при этом уравнение (10.8) становится существенно проще). Т.е. функция v (x) является произвольным частным решением дифференциального уравнения 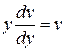 с разделяющимися переменными.
с разделяющимися переменными.
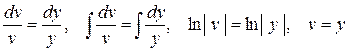 .
.
2) Подставляя 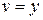 в уравнение (10.8), найдем функцию u (x):
в уравнение (10.8), найдем функцию u (x):
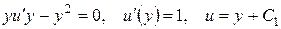 . Таким образом, общим решением дифференциального уравнения (10.8) является
. Таким образом, общим решением дифференциального уравнения (10.8) является 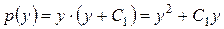 . Вспоминая о том, что
. Вспоминая о том, что 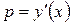 , мы приходим к дифференциальному уравнению первого порядка
, мы приходим к дифференциальному уравнению первого порядка 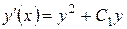 , из которого найдем
, из которого найдем 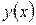 :
:
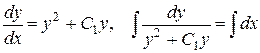 . Интегрируя последнее равенство, мы находим общий интеграл исходного дифференциального уравнения:
. Интегрируя последнее равенство, мы находим общий интеграл исходного дифференциального уравнения:
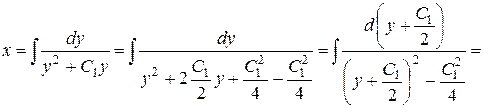
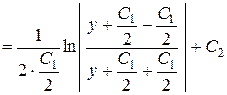 и, следовательно,
и, следовательно, 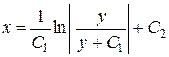 .
.
 2015-04-01
2015-04-01 899
899








