1. Рассмотрим свободную частицу с массой 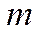 и гамильтонианом
и гамильтонианом 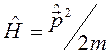 . Очевидно, что оператор импульса
. Очевидно, что оператор импульса 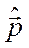 коммутирует с гамильтонианом, что приводит к сохранению импульса частицы. При этом сохраняется также и энергия частицы.
коммутирует с гамильтонианом, что приводит к сохранению импульса частицы. При этом сохраняется также и энергия частицы.
2. Другой пример-движение частицы в поле с центральной симметрией. Гамильтониан такой системы имеет вид
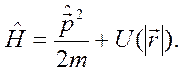
Выясним, сохраняется ли момент импульса частицы? Оператор момента импульса определяется как 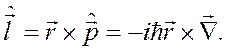
Покажем, что оператор квадрата импульса в сферической системе координат можно представить в виде
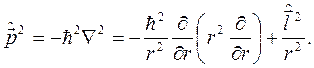 (2.33)
(2.33)
где, согласно, (1.39)
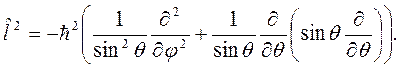
С другой стороны, по определению
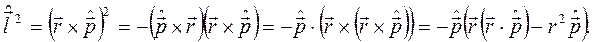
Далее воспользуемся коммутационными соотношениями между операторами координаты и импульса 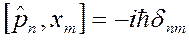 и вычислим коммутаторы
и вычислим коммутаторы
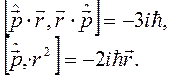
Используя полученные выражения, преобразуем оператор 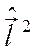 к виду
к виду
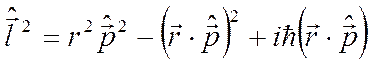
(2.34)
Входящие в это выражение скалярные произведения 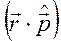 и
и 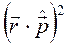 соответственно равны
соответственно равны
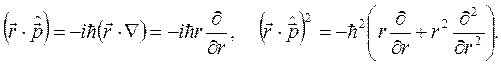 (2.35)
(2.35) 
Подстановка (2.30)  в (2.29) приводит к представлению (2.28). Таким образом, получаем, что оператор квадрата момента импульса коммутирует с оператором квадрата импульса. Учитывая также, что
в (2.29) приводит к представлению (2.28). Таким образом, получаем, что оператор квадрата момента импульса коммутирует с оператором квадрата импульса. Учитывая также, что 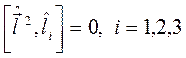 и операторы
и операторы 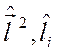 в сферической системе координат зависят только от угловых переменных (см. формулы (1.37)-(1.39)) и поэтому коммутируют с
в сферической системе координат зависят только от угловых переменных (см. формулы (1.37)-(1.39)) и поэтому коммутируют с 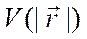 .
.
Окончательно, в задаче о движении частицы в центральном поле интегралами движения являются 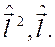
 2015-04-17
2015-04-17 455
455








