2015-04-17
377
Пусть свойства системы инвариантны относительно группы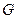 
непрерывных преобразований координат
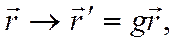
где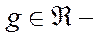 
параметр. Закон преобразования волновой функции принимает вид
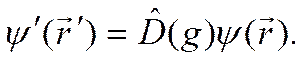
Линейные операторы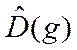 
реализуют представление группы 
.
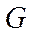Рассмотрим группу трансляций
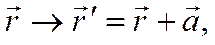
где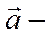 
постоянный вектор. Имеем
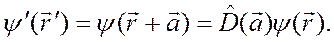
Разложим функцию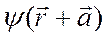 
в ряд по степеням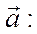 
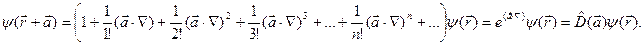Или
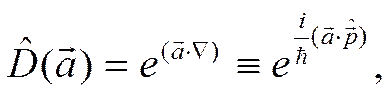
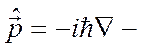оператор импульса.
Таким образом,
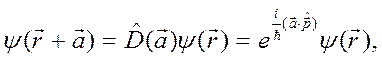
т.е. оператор импульса является генератором группы трансляций в пространстве волновых функций.
Для свободной частицы оператор импульса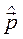 
коммутирует с гамильтонианом 
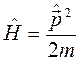, так, что импульс частицы есть интеграл движения.
Рассмотрим группу вращений в трехмерном пространстве (обозначение SO (3)). Закон преобразования в этом случае имеет вид
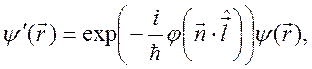
где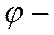 
угол поворота вокруг оси, направление которой задано единичным вектором 
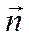, а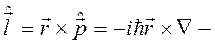 
оператор момента импульса.
Таким образом, оператор момента импульса является генератором группы вращений SO (3). В предыдущем разделе было установлено, что для частицы в центральном поле момент импульса сохраняется, т.е. является интегралом движения.
