Не вдаваясь в подробности, обсудим связь интегралов движения с симметрией системы. Предположим, что гамильтониан системы не зависит явно от времени. Пусть спектр гамильтониана не меняется при преобразовании волновой функции
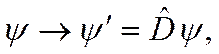
где 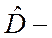 линейный оператор. Инвариантность означает, что из уравнения
линейный оператор. Инвариантность означает, что из уравнения 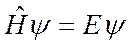 , следует аналогичное уравнение для преобразованной функции
, следует аналогичное уравнение для преобразованной функции 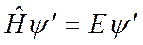 или
или 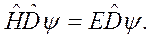 Отсюда следует
Отсюда следует 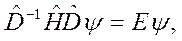 где
где 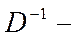 обратный оператор. Оператор
обратный оператор. Оператор 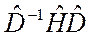 слева, стоящий перед функцией
слева, стоящий перед функцией 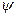 совпадает с гамильтонианом
совпадает с гамильтонианом 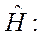
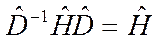 или
или 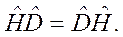
Условие инвариантности означает, таким образом, коммутацию гамильтониана с оператором 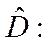
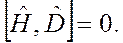 (2.31)
(2.31) 
Естественно также предположить сохранение нормы векторов 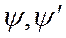
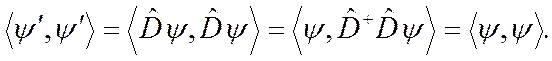
Отсюда следует, что оператор преобразования 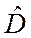 должен быть унитарным
должен быть унитарным
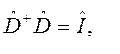 или
или 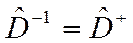 .
.
Здесь 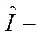 единичный оператор. Часто в приложениях используются унитарные операторы вида
единичный оператор. Часто в приложениях используются унитарные операторы вида
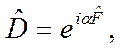 (2.32)
(2.32)
где 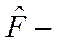 эрмитов оператор (
эрмитов оператор (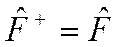 ),
), 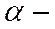 действительный параметр.
действительный параметр.
С учетом (2.32) условие инвариантности принимает вид
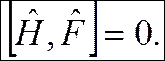 (2.33)
(2.33)
Следовательно, физическая величина, которой соответствует оператор 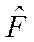 -есть интеграл движения (
-есть интеграл движения (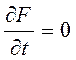 ).
).
 2015-04-17
2015-04-17 734
734








