Задание. 1. Показать, что нормировка волновой функции, удовлетворяющей уравнению Шредингера, не изменяется со временем

1. Показать, что нормировка волновой функции, удовлетворяющей уравнению Шредингера, не изменяется со временем.

2. Показать, что операторы скорости и ускорения частицы, движущейся в поле с потенциальной энергией 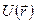могут быть представлены в виде

,

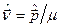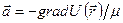
где 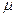— масса частицы, 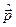— оператор ее импульса.

3. Частица находится в состоянии, описываемом в сферических координатах волновой функцией

,

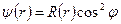где 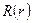— некоторая квадратично интегрируемая функция. Найти распределение проекции момента количества движения на ось .

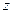4. Доказать, что в любом состоянии распределение любой сохраняющейся величины не меняется со временем.

5. Построить оператор плотности распределения координаты частицы, движущейся в заданном поле.