Функции распределения времени пребывания идеальных и неидеальных проточных реакторов

Реактор идеального смешения.

Выведем уравнение, позволяю­щее рассчитать интегральную функцию распределения F(τ) для сгационарного реактора идеального смешения, а затем дифферен­цированием этой функции получим дифференциальную функцию распределения f (τ).

Всоответствии с допущениями об идеальности, любой бес­конечно малый элемент потока, вошедший в реактор идеального смешения, может сразу после ввода появиться с вероятностью f (τ₀+Δτ) в любой точке реактора или в потоке, выходящем из ре­актора. Следовательно, вероятность выхода такого элемента из реактора не зависит от его пути или его истории (длительности пребывания в реакторе). Поэтому вероятность того, что он оста­нется в аппарате дольше, чем в течение времени τ +Δτ, равна про­изведению вероятностей двух взаимно независимых событий:

1) время пребывания в реакторе больше чем τ;

2) время пребыва­ния в реакторе больше чем Δτ.

Вероятность первого события равна [1 - F(τ)] вероятность вто­рого [1 - F(Δτ)]. Тогда

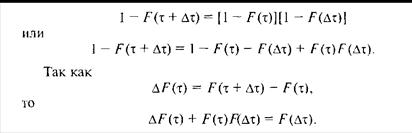(12.5)

По определению, F(Δτ) – это объемная доля потока, находя­щаяся в реакторе в течение времени, меньшего чем Δτ.

С другой стороны, за время Δτ из реактора выйдет реакционная смесь объемом v Δτ. Вероятность выхода из аппарата одинакова для всех элементов объема реактора идеального смешения. Поэтому

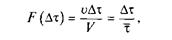
где 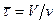– среднее время пребывания в реакторе.

Подставляя F(Δτ) в уравнение (12.5) при Δτ, стремящемся к бес­конечно малому приращению d τ, ΔF(τ) → dF(τ) получим диффе­ренциальное уравнение

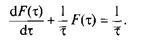(12.6)

Найдем его частное решение при начальном условии

F(0) = 0 (12.7)

Уравнение (12.6) – дифференциальное уравнение первого по­рядка с разделяющимися переменными. Представим его в следую­щем виде:

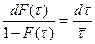(12.8)

После интегрирования получим

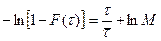(12.9)

Путем несложных преобразований уравнения (12.9) можно привести к виду

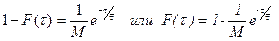
В соответствии с начальным условием (12.7) постоянная интег­рирования равна единице (M = 1). Окончательно имеем

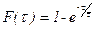(12.10)

Плотность распределения времени пребывания f (τ) может быть получена дифференцированием уравнения (12.10):

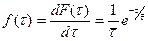(12.11)

Графики функций F(τ) и f (τ) приведены на рис. 12.5.

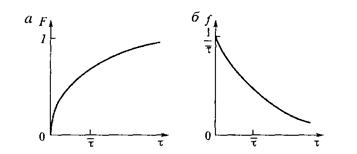
Рис. 12.5. Интегральная (а) и дифференциальная (б) функции распределе­ния

времени пребывания в проточном реакторе идеального смешения

Реактор идеального вытеснения.

При плоском профиле линей­ных скоростей все частицы должны находиться и реакторе строго одинаковое время, равное среднему времени пребывания 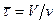. Следовательно, для всех 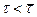функция F(τ) = 0 и для всех 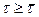функция F(τ) = 1.

Таким образом, интегральная функция распределения F(τ) для реактора идеального вытеснения – это разрывная функция, имею­щая только два значения; 0 и 1 (рис. 12.6, а).

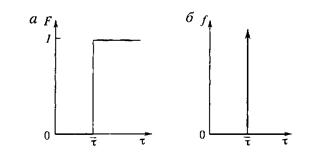
Рис. 12.6. Интегральная (а) и дифференциальиая (б)функции распреде­ления

времени пребывания в проточном реакторе идеального вытеснения

Для получения дифференциальной функции распределения нужно продифференцировать F(τ). Производная в точке разрыва (скачка) функции является особой функцией, называемой дельта- функцией Дирака 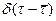, которую изучают в специальных разделах математики (рис. 12.6, б). Таким образом, используя дельта функцию можно записать

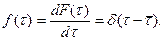
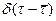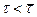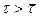δ -функция обладает особыми свойствами. Функция равна нулю при всех значениях и . При 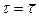функция 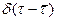= δ (0) = ∞.

δ -функция Дирака относится к классу обобщенных функций, изучаемых н специальных разделах математики.

Кроме того, функция 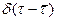должна удовлетворять условию

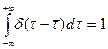(12.12)

Так как отрицательные значения τ не имеют физического смысла, то нижний предел интегрирования в уравнении (12.12), сле­дует заменить на τ = 0. Тогда полученное уравнение

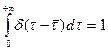
совпадает с одним из свойств дифференциальной функции рас­пределения [см. уравнение (12.1)].

Можно представить график функции, похожей на 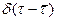(рис. 12.7). Чем более узкой будет полоска между левой и правой ветвями, тем выше должна быть эта полоска, чтобы ее площадь (т. е. интеграл) сохраняла заданное значение, равное 1. Такой вид, в частности, будет иметь дифференциальная функция распределения времени пребывания для реального трубчатого реактора, гидродинамиче­ский режим в котором приближается к идеальному вытеснению.

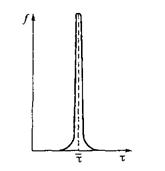
Рис. 12.7. Функция, приближающаяся по свойствам к δ -функции

Конечно, δ -функция является определенной идеализацией, как, впрочем, идеализацией является и режим полного вытесне­ния, для описания которого она может быть применена.