2015-04-01
315
Рассмотрим уравнения вида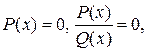 
где 
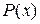и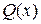 
- многочлены, а так же уравнения вида 
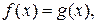где 
и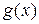 
- рациональные выражения.
Напомним некоторые сведения из алгебры.
1. Если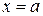 
корень многочлена 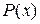, то 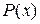делится без остатка на двучлен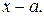 
2. Пусть все коэффициенты многочлена 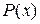- целые числа, причем старший коэффициент равен 
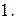Если такой многочлен имеет своим корнем рациональное число, то это число целое.
3. Пусть коэффициенты многочлена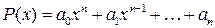 
- целые числа. если корнем многочлена является целое число 
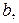то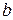 
– делитель свободного члена 
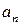(необходимое условие существования целочисленного корня).
Отметим, что при решении целых рациональных уравнений преобразования, выполняемые в процессе решения, приводят только к уравнениям, равносильным заданному. Поэтому, естественно, найденные корни не проверяют и упоминать об этом не следует. При решении же дробно-рациональных уравнений выполняется умножение обеих частей на одно и тоже выражение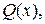 
что может привести к появлению посторонних корней. Поэтому при решении дробно-рациональных уравнений проверка необходима.
При решении рациональных (и других) уравнений основными являются следующие методы:
1) разложение на множители;
2) введение новых переменных.
Метод разложения на множители заключается в следующем: если
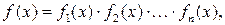
то всякое уравнение
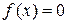(1)
является решением совокупности уравнений
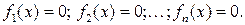(2)
Обратное утверждение, вообще говоря, неверно: не всякое решение совокупности (2) является решением уравнения (1).
