Пример 1. Решим уравнение 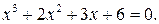
Решение. Разложим левую часть уравнения на множители. Имеем 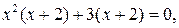 и далее
и далее 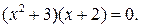
Последнее уравнение равносильно совокупности уравнений
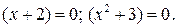
Из первого уравнения получаем 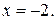 Второе уравнение не имеет действительных корней.
Второе уравнение не имеет действительных корней.
Ответ: 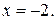
Пример 2. Решим уравнение 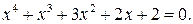
Решение. Попытки выполнить в левой части уравнения группировку аналогичную тому, как это было сделано в примере 1, оказываются неудачными. Поэтому попытаемся какой-нибудь член уравнения представить в виде суммы нескольких слагаемых таким образом, чтобы группировка, позволяющая получить «удачное» разложение на множители, была осуществима. Положим 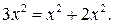 Тогда получим
Тогда получим 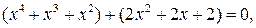 и далее
и далее
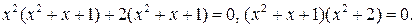
Остается решить совокупность уравнений
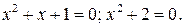
Ни одно из них действительных корней не имеет. Значит, заданное уравнение не имеет действительных корней.
Пример 3. Решим уравнение 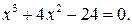
Решение. Можно попытаться решить это уравнение, как в предыдущих примерах 1 и 2, разложением на множители (представив 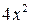 в виде суммы
в виде суммы 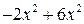 , получить уравнение
, получить уравнение 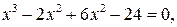 а затем
а затем 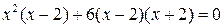 и т.д.). Мы покажем на этом примере так называемый метод подбора, с помощью которого отыскивается целый корень уравнения. Используя необходимое условие существования целочисленного корня, выпишем делители свободного члена:
и т.д.). Мы покажем на этом примере так называемый метод подбора, с помощью которого отыскивается целый корень уравнения. Используя необходимое условие существования целочисленного корня, выпишем делители свободного члена:
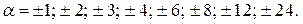
Теперь начинаем пробы. Подставим вместо 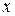 в данное уравнение
в данное уравнение 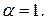 Получаем
Получаем 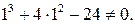
Таким образом 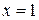 не является корнем уравнения. Продолжаем пробы:
не является корнем уравнения. Продолжаем пробы: 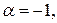
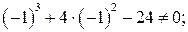
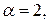
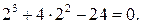 Итак
Итак 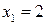 - корень уравнения.
- корень уравнения.
Воспользуемся тем, что многочлен 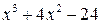 делится без остатка на
делится без остатка на 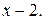 Выполним это деление:
Выполним это деление:
 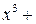
| 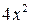
| 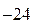
| 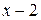
| |
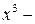
| 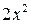
| 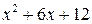
| ||
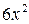
| ||||
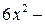
| 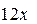
| |||
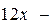
| 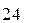
| |||
 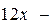
| 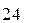
| |||
Таким образом, 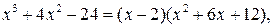 а, значит, исходное уравнение принимает вид:
а, значит, исходное уравнение принимает вид:
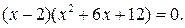
Это уравнение равносильно совокупности уравнений (решение первого из которых уже найдено) 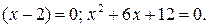 Второе уравнение совокупности не имеет корней.
Второе уравнение совокупности не имеет корней.
Заданное уравнение имеет один действительный корень 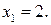
Пример 4. Решим уравнение 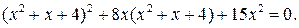
Решение. Положим 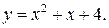 Тогда заданное уравнение примет вид:
Тогда заданное уравнение примет вид:
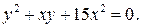
Решим это уравнение как квадратное относительно 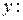
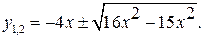
Итак, 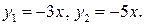 Таким образом, задача сводится к решению следующей совокупности уравнений:
Таким образом, задача сводится к решению следующей совокупности уравнений:
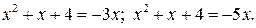
Из этой совокупности находим: 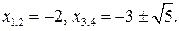
Пример 5. Решим уравнение 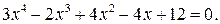
Решение. Заданное уравнение имеет интересную особенность: отношение первого коэффициента к свободному члену и квадрат отношения второго коэффициента к предпоследнему равны между собой. Уравнения с такой особенностью называются возвратными. На этом примере мы покажем способ решения возвратного уравнения четвертой степени.
Разделив обе части уравнения на 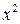 (это не приведет к потере корня, так как значение
(это не приведет к потере корня, так как значение 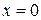 не является корнем заданного уравнения). Получим:
не является корнем заданного уравнения). Получим:
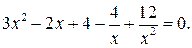
и далее
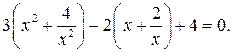
Положим 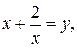 тогда
тогда 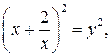 а потому
а потому 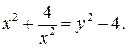 Заменив в последнем уравнении
Заменив в последнем уравнении 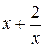 на
на 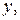 а
а 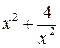 на
на 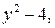 получим:
получим: 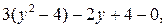 откуда находим
откуда находим 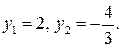
Теперь задача свелась к решению совокупности уравнений:
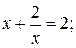
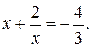
Эти уравнения не имеют действительных корней, значит, и заданное уравнение не имеет корней.
 2015-04-01
2015-04-01 535
535








