Пример 1. Решим уравнение 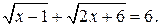
Решение. Возведем обе части уравнения в квадрат:
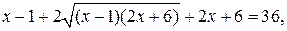
и далее
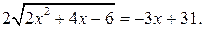
После возведения в квадрат последнего уравнения получим: 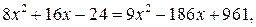
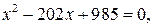 откуда находим
откуда находим 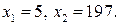
Проверка. Найденные корни несложно проверить непосредственной подстановкой в исходное уравнение.
1) 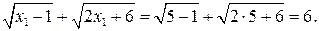
Таким образом, 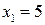 является корнем заданного уравнения.
является корнем заданного уравнения.
2) 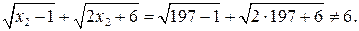 т.е.
т.е. 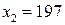 – посторонний корень. Таким образом, только
– посторонний корень. Таким образом, только 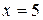 является корнем заданного уравнения.
является корнем заданного уравнения.
Ответ. 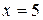
Пример 2. Решим уравнение 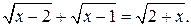
Решение. Возведем обе части уравнения в квадрат и уединим затем полученный радикал:
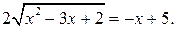 (*)
(*)
После возведения в квадрат обеих частей последнего уравнения и последующего приведения подобных членов получим квадратное уравнение: 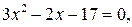 корнями которого являются
корнями которого являются 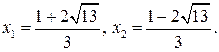
Проверка. Проверять найденные корни подстановкой в уравнение явно нецелесообразно. Поступим следующим образом. Найдем область определения исходного уравнения. Из системы неравенств
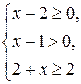
находим, что этой областью является луч 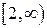 . Выясним, принадлежат ли найденные корни этому лучу. Имеем:
. Выясним, принадлежат ли найденные корни этому лучу. Имеем: 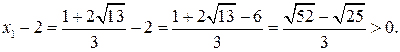
Таким образом, 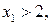 т.е.
т.е. 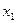 принадлежит лучу
принадлежит лучу 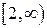 , и, значит,
, и, значит, 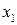 может являться корнем уравнения. Далее,
может являться корнем уравнения. Далее, 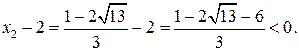
Таким образом, 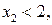 т.е.
т.е. 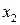 не принадлежит лучу
не принадлежит лучу 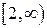 , и, значит,
, и, значит, 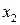 не являться корнем уравнения.
не являться корнем уравнения.
Вернемся теперь к 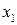 . Выясним знак разности, находящейся в правой части уравнения. Имеем:
. Выясним знак разности, находящейся в правой части уравнения. Имеем: 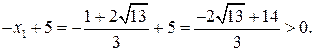
Таким образом, 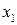 являться корнем уравнения (*). А так как уравнение (*) равносильно данному уравнению, то корнями уравнения (*) могут являться только корни исходного уравнения. Итак, корнем уравнения является
являться корнем уравнения (*). А так как уравнение (*) равносильно данному уравнению, то корнями уравнения (*) могут являться только корни исходного уравнения. Итак, корнем уравнения является 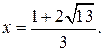
Ответ. 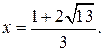
Пример 3. Решим уравнение 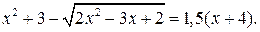
Решение. Уединение корня и возведение обеих частей уравнения привели бы к громоздкому уравнению. В то же время, если проявить некоторую наблюдательность, можно заметить, что уравнение легко сводится к квадратному. Действительно, умножив обе его части на 2, получим: 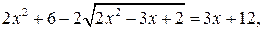 и далее
и далее 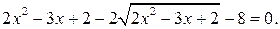
Положив 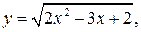 получим
получим 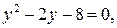 откуда
откуда 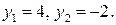 Значит, уравнение равносильно следующей совокупности уравнений:
Значит, уравнение равносильно следующей совокупности уравнений:
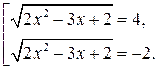
Из первого уравнения совокупности находим 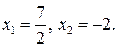
Второе уравнение корней не имеет.
Проверка. Так как совокупность уравнений равносильна уравнению, причем второе уравнение этой совокупности корней не имеет, то найденные корни можно проверить подстановкой в уравнение 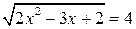 . Эта подстановка показывает, что оба найденных значения
. Эта подстановка показывает, что оба найденных значения 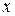 являются корнями этого уравнения, а значит, и заданного уравнения.
являются корнями этого уравнения, а значит, и заданного уравнения.
Ответ. 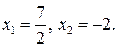
Пример 4. Решим уравнение 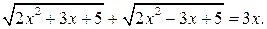 (*)
(*)
Решение. Умножим обе части заданного уравнения на выражение 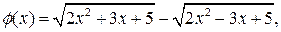 сопряженное выражению
сопряженное выражению 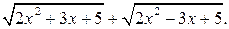 Так как
Так как
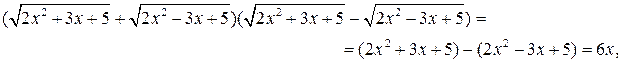
то уравнение примет вид: 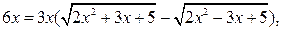 или
или 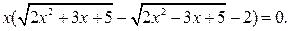
Как легко видеть, 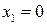 является корнем этого уравнения. Остается решить уравнение
является корнем этого уравнения. Остается решить уравнение 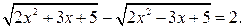 (**)
(**)
Сложив уравнения (*) и (**), придем к уравнению 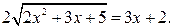 Решая уравнение методом возведения в квадрат, получим:
Решая уравнение методом возведения в квадрат, получим: 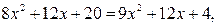 и далее
и далее 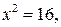 откуда
откуда 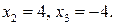
Проверка. Поочередно подставляя найденные значения 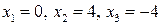 в исходное уравнение, убеждаемся, что ему удовлетворяет только значение
в исходное уравнение, убеждаемся, что ему удовлетворяет только значение 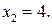 Таким образом,
Таким образом, 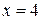 - единственный корень уравнения.
- единственный корень уравнения.
Ответ. 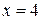 .
.
 2015-04-01
2015-04-01 416
416








