Пример 1. Решим уравнение 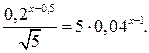
Решение. Приведем все степени к одинаковому основанию 5:
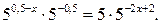
Далее получаем уравнение 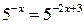 , которое равносильно уравнению
, которое равносильно уравнению 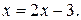 Корнем этого уравнения, а, значит, и корнем заданного уравнения является
Корнем этого уравнения, а, значит, и корнем заданного уравнения является 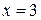 .
.
Ответ. 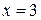 .
.
Пример 2. Решим уравнение 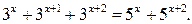
Решение. Так как 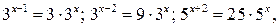 то заданное уравнение перепишем в виде
то заданное уравнение перепишем в виде 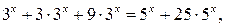 или
или 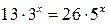 , т.е.
, т.е. 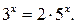 Далее имеем
Далее имеем 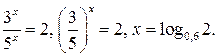
Ответ. 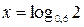 .
.
Пример 3. Решим уравнение 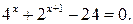
Решение. Так как 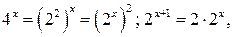 то заданное уравнение можно переписать следующим образом:
то заданное уравнение можно переписать следующим образом:
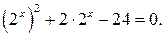
Введем новую переменную, положив 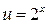 , и решим полученное уравнение
, и решим полученное уравнение 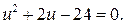 Его корнями являются
Его корнями являются 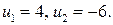 Таким образом, решение заданного уравнения сводится к решению совокупности уравнений:
Таким образом, решение заданного уравнения сводится к решению совокупности уравнений:
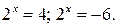
Из первого уравнения этой совокупности получаем 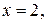 а второе уравнение корней не имеет, так как
а второе уравнение корней не имеет, так как 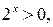 а
а 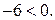 Итак,
Итак, 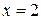 - корень заданного уравнения.
- корень заданного уравнения.
Ответ. 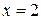 .
.
Пример 4. Решим уравнение 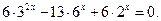
Решение. Так как 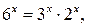 то имеем:
то имеем:
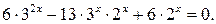
Положив 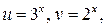 получим уравнение
получим уравнение
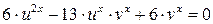 , (*)
, (*)
которое является однородным уравнением второй степени относительно переменных 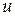 и
и 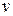 .
.
Так как 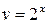 ни при каких значениях
ни при каких значениях 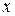 не обращается в нуль, то, разделив обе части уравнения (*) на
не обращается в нуль, то, разделив обе части уравнения (*) на 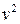 , получим уравнение равносильное уравнению (2):
, получим уравнение равносильное уравнению (2):
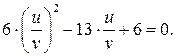
Полагая 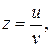 получим:
получим:
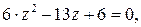 откуда
откуда 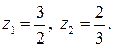
Учитывая, что 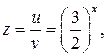 запишем совокупность уравнений:
запишем совокупность уравнений:
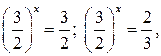
из которой находим 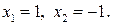 Значит заданное уравнение имеет два корня:
Значит заданное уравнение имеет два корня: 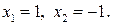
Ответ. 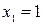 ,
, 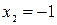 .
.
Пример 5. Решим неравенство 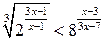 .
.
Решение. Преобразуем неравенство к виду
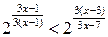
По теореме 2 данное неравенство равносильно неравенству
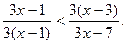
Решим полученное неравенство:
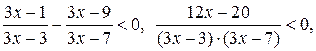
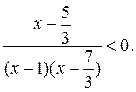
Из последнего неравенства методом интервалов получаем 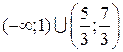 .
.
Ответ. 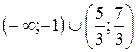 .
.
Пример 6. Решим неравенство
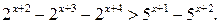
Решение. Последовательно получаем:
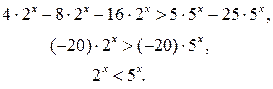
Разделив обе части последнего неравенства на 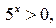 получим равносильное неравенство
получим равносильное неравенство 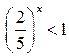 , или
, или 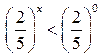 . Здесь основание
. Здесь основание 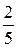 удовлетворяет двойному неравенству
удовлетворяет двойному неравенству 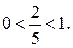 Значит по теореме 3 неравенство
Значит по теореме 3 неравенство
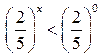
равносильно неравенству 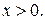 Итак, промежуток
Итак, промежуток 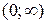 является решением неравенства (3).
является решением неравенства (3).
Ответ. 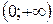 .
.
Пример 7. Решим неравенство 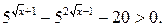
Решение. Перепишем это неравенство следующим образом:
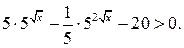
После замены 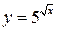 получим неравенство
получим неравенство
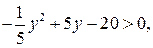
и далее 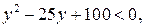 или
или 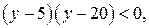 откуда
откуда 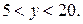
Таким образом, решение заданного неравенства сводится к решению системы неравенств
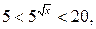 или
или 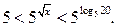
Эта система равносильна (так как основание 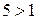 ) системе
) системе 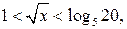 откуда
откуда 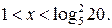
Итак, промежуток 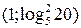 является решением заданного неравенства.
является решением заданного неравенства.
Ответ. 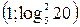 .
.
 2015-04-01
2015-04-01 402
402








