Рассмотрим поверхностный эффект на примере падения плоской электромагнитной волны на полуограниченное металлическое тело с плоской поверхностью (рис. 1.3). Будем считать, что размеры поверхности и глубина тела бесконечны, а его физические свойства постоянны во всех точках. Этот весьма идеализированный случай тем не менее очень важен для рассмотрения электромагнитных явлений в реальных проводниках при ярко выраженном поверхностном эффекте.
  |
| Рис. 1.3. Ориентация векторов поля плоской электромагнитной волны на поверхности полуограниченного пространства |
Запишем допущения для этого случая:
1. Поле принимается квазистационарным. Это означает, что нет запаздывания электромагнитной волны в воздухе (но не в металле; в металле запаздывание электромагнитной волны есть).
В иной формулировке: длина электромагнитной волны в воздухе много больше максимального геометрического размера системы.
2. Расчет установившихся электромагнитных процессов можно проводить для величин, изменяющихся во времени по гармоническому закону. При этом ошибка в определении интегральных и распределенных параметров не велика. Это позволяет использовать символический метод при выводе формул и расчетах на ЭВМ электромагнитных процессов.
3. Потери на гистерезиспри нагреве ферромагнитных тел много меньше, чем на вихревые потери. Поэтому принимается, что зависимость 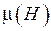 — однозначная и вещественная величина.
— однозначная и вещественная величина.
4. Потери на гистерезис и вихревые токи в магнитопроводе не оказывают влияние на электромагнитное поле вне его, и их можно учитывать отдельно при расчете теплового режима магнитопровода.
5. Размеры полуограниченного пространства с плоской поверхностью много больше глубины проникновения.
6. Свойства материала — магнитная проницаемость 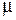 и удельное сопротивление
и удельное сопротивление 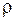 — постоянны во всем исследуемом объеме.
— постоянны во всем исследуемом объеме.
7. Граничные условия: напряженность магнитного поля на границе, разделяющей металл и воздух, одинакова и равна 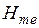 .
.
Принятые допущения позволяют решать одномерную электромагнитную задачу для полуограниченного пространства (рис. 1.3), свойства которого постоянны во всем исследуемом объеме [1–3].
Уравнения и выражают в дифференциальной форме законы полного тока и электромагнитной индукции соответственно. Второе слагаемое в правой части уравнения представляет собой плотность тока смещения, которым в проводнике практически всегда можно пренебречь.
Так как в плоской волне векторы 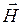 и
и 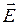 имеют лишь по одной составляющей (в рассматриваемом случае
имеют лишь по одной составляющей (в рассматриваемом случае 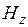 и
и 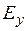 — см. рис. 1.3.), то уравнения и упростятся:
— см. рис. 1.3.), то уравнения и упростятся:
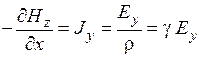 ,
,
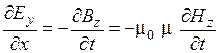 ,
,
где 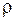 — удельное сопротивление, Ом·м;
— удельное сопротивление, Ом·м; 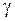 — удельная проводимость, 1/(Ом·м).
— удельная проводимость, 1/(Ом·м).
В дальнейшем индексы «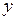 » и «
» и «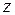 » будут опускаться. Если
» будут опускаться. Если 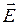 и
и 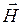 — синусоидальные функции времени, то
— синусоидальные функции времени, то
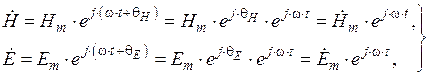
где 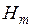 и
и 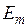 ,
, 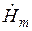 и
и 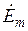 — вещественные и комплексные амплитуды напряженности магнитного и электрического полей соответственно;
— вещественные и комплексные амплитуды напряженности магнитного и электрического полей соответственно; 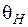 и
и 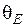 — соответствующие начальные фазы;
— соответствующие начальные фазы; 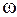 — круговая частота.
— круговая частота.
Подставляя выражения в уравнения и, получим:
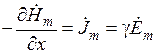 ,
,
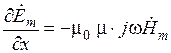 ,
,
После подстановки в уравнение выражения для 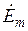 из уравнения, получим:
из уравнения, получим:
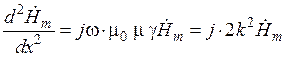 ,
,
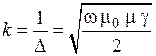 ,
,
где 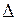 — глубина проникновения тока, м:
— глубина проникновения тока, м:
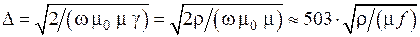 .
.
Решение уравнения имеет вид:
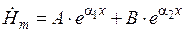 .
.
Коэффициенты 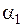 и
и 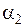 находятся из характеристического уравнения, они равны:
находятся из характеристического уравнения, они равны:
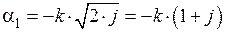 ,
,
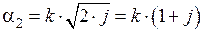 .
.
Выражение для 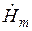 может содержать только слагаемое с отрицательным коэффициентом
может содержать только слагаемое с отрицательным коэффициентом 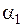 , так как в противном случае
, так как в противном случае 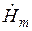 будет неограниченно возрастать с возрастанием
будет неограниченно возрастать с возрастанием 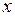 , что невозможно.
, что невозможно.
Таким образом, решение будет иметь вид:
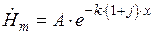 .
.
При 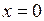 имеем
имеем 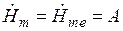 , т.е. амплитуда напряженности равна своему значению на поверхности
, т.е. амплитуда напряженности равна своему значению на поверхности 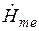 . Выбрав начало отсчета времени так, что при
. Выбрав начало отсчета времени так, что при 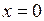 значение
значение 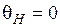 , получим
, получим 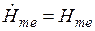 . Тогда выражение для
. Тогда выражение для 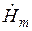 примет вид:
примет вид:
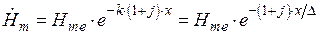 .
.
Из уравнения определим:
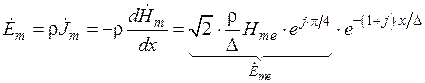 .
.
Отсюда можно найти выражение для плотности тока:
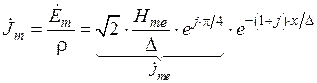 .
.
Понятие глубины проникновения 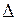 в выражениях – очень важно. В слое толщиной
в выражениях – очень важно. В слое толщиной 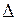 проходит примерно 85,89% полного тока и выделяется 86,5% мощности. Использование понятия глубины проникновения часто позволяет упростить расчеты, заменив экспоненциальное распределение — более простым, прямоугольным, т.е. считать, что весь ток течет только в слое глубиной
проходит примерно 85,89% полного тока и выделяется 86,5% мощности. Использование понятия глубины проникновения часто позволяет упростить расчеты, заменив экспоненциальное распределение — более простым, прямоугольным, т.е. считать, что весь ток течет только в слое глубиной 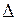 с равномерной плотностью
с равномерной плотностью 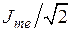 , и за пределами этого слоя плотность тока равна нулю. Это значит, что при тепловом расчете индукционного нагрева плоской заготовки, размеры которой много больше глубины проникновения, можно считать, что энергия выделяется в слое
, и за пределами этого слоя плотность тока равна нулю. Это значит, что при тепловом расчете индукционного нагрева плоской заготовки, размеры которой много больше глубины проникновения, можно считать, что энергия выделяется в слое 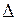 и распределена в нем равномерно.
и распределена в нем равномерно.
Кроме того, довольно просто определяется внутреннее электрическое сопротивление параллелепипеда длиной 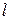 , шириной
, шириной 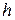 и толщиной Ос (рис. 1.3):
и толщиной Ос (рис. 1.3):
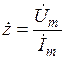 .
.
Воспользовавшись законом электромагнитной индукции для контура OcefO на рис. 1.3 и полного тока для контура OabcO, получим:
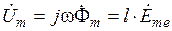 ,
,
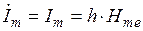 .
.
Подставив выражения для 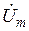 и
и 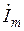 , получим:
, получим:
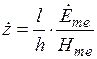 .
.
Подставив выражение для 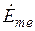 из, получим:
из, получим:
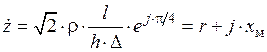 .
.
Необходимо иметь в виду, что 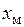 — внутреннее индуктивное сопротивление параллелепипеда, оно определяется магнитным потоком, проходящим внутри металла (поэтому использован индекс «м»).
— внутреннее индуктивное сопротивление параллелепипеда, оно определяется магнитным потоком, проходящим внутри металла (поэтому использован индекс «м»).
Модуль электрического сопротивления, а также активное и внутреннее индуктивное сопротивления равны:
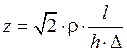 ,
, 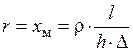 .
.
Здесь выступает физический смысл 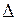 : электрическое сопротивление полубесконечной среды при тех допущениях, которые мы приняли, равно сопротивлению полосы толщиной
: электрическое сопротивление полубесконечной среды при тех допущениях, которые мы приняли, равно сопротивлению полосы толщиной 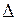 .
.
Важными частными случаями формулы для глубины проникновениями, широко используемыми на практике, являются:
1) Глубина проникновения в материал индуктора — медь.
Для меди 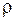 =2∙10–8 Ом∙м,
=2∙10–8 Ом∙м, 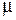 =1. Тогда:
=1. Тогда:
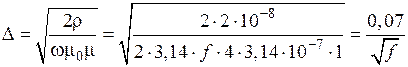 .
.
2) Глубина проникновения в металл при 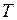 >750 °C.
>750 °C.
В этом случае 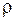 = 10–6 Ом·м и
= 10–6 Ом·м и 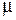 =1. Тогда:
=1. Тогда:
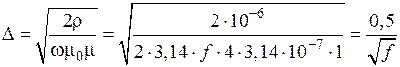 .
.
1.2.2. Распределение параметров электромагнитного поля в проводящем цилиндре при ярко выраженном поверхностном эффекте (R 2 >> D2)
При расчете параметров электромагнитного поля в системе индуктор – нагреваемый цилиндр все геометрические и электрические параметры для индуктора обозначены с индексом «1» (D 1, R 1, h 1, D1, r1 и т.д.), а для цилиндра – с индексом «2» (D 2, R 2, h 2, D2, r2 и т.д.).
а) Цилиндр с постоянными электрическими параметрами по всему объему (r=const, m=const)
При решении электромагнитной задачи для цилиндра при ярко выраженном поверхностном эффекте могут быть использованы распределения напряженностей магнитного и электрического полей, а также плотности тока для полубесконечной среды:
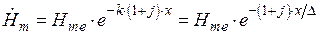 ,
,
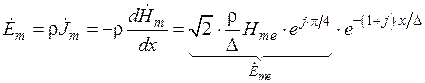 ,
,
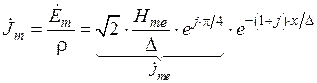 ,
,
где 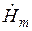 ,
, 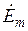 ,
, 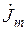 —комплексные значения амплитуд напряженностей магнитного (А/м) и электрического (В/м) полей и плотности тока (А/м2) внутри цилиндра на расстоянии
—комплексные значения амплитуд напряженностей магнитного (А/м) и электрического (В/м) полей и плотности тока (А/м2) внутри цилиндра на расстоянии 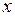 от поверхности цилиндра;
от поверхности цилиндра; 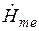 ,
, 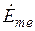 ,
, 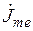 —комплексные значения амплитуд напряженностей магнитного (А/м) и электрического (В/м) полей и плотности тока (А/м2) на поверхности цилиндра (при этом начало отсчета времени выбрано так, что при
—комплексные значения амплитуд напряженностей магнитного (А/м) и электрического (В/м) полей и плотности тока (А/м2) на поверхности цилиндра (при этом начало отсчета времени выбрано так, что при 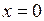 и
и 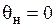 получаем:
получаем: 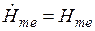 );
); 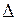 — глубина проникновения тока,
— глубина проникновения тока, 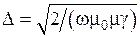 (на глубине
(на глубине 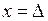 параметры
параметры 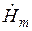 ,
, 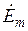 и
и 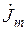 уменьшаются в
уменьшаются в 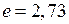 раз).
раз).
Зависимости 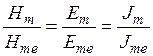 от относительной глубины
от относительной глубины 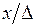 приведены на рис. 1.4, а распределения плотности тока по сечению нагреваемого предмета изображены на рис. 1.5.
приведены на рис. 1.4, а распределения плотности тока по сечению нагреваемого предмета изображены на рис. 1.5.
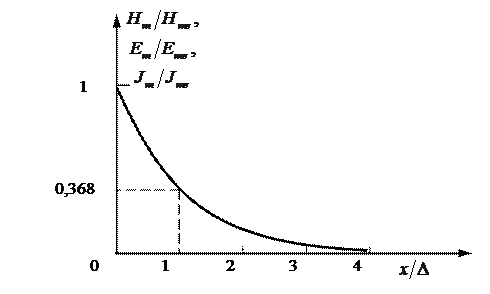
Рис. 1.4. Зависимость плотности тока, напряженностей электрического и магнитного полей от глубины для
полубесконечной среды и цилиндра при ярко
выраженном поверхностном эффекте (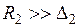 )
)
Использование понятия глубины проникновения тока при ярко выраженном поверхностном эффекте ( ) позволяет упростить расчеты. Экспоненциальное распределение тока можно заменить более простым — прямоугольным, т.е. считать, что ток течет только в слое глубиной
) позволяет упростить расчеты. Экспоненциальное распределение тока можно заменить более простым — прямоугольным, т.е. считать, что ток течет только в слое глубиной 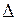 на поверхности цилиндра с равномерной плотностью
на поверхности цилиндра с равномерной плотностью 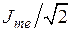 , и за пределами этого слоя равен нулю. Тепловой расчет для данного случая может производиться при допущении, что вся энергия выделяется в слое глубиной
, и за пределами этого слоя равен нулю. Тепловой расчет для данного случая может производиться при допущении, что вся энергия выделяется в слое глубиной 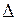 (глубина активного слоя).
(глубина активного слоя).
Полное электрическое сопротивление элемента на поверхности цилиндра длиной 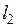 , шириной
, шириной 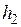 и глубиной много больше
и глубиной много больше 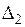 с постоянными параметрами (r=const, m=const), так же как и для полубесконечной среды:
с постоянными параметрами (r=const, m=const), так же как и для полубесконечной среды:
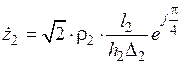 ,
,
и модуль:
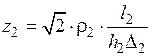 .
.
При этом активное и внутреннее реактивное сопротивление для цилиндра диаметром 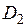 и длиной
и длиной 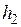 :
:
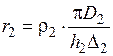 ,
,
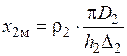 .
.
 2015-04-01
2015-04-01 1149
1149








