При решении электромагнитной задачи для цилиндра из ферромагнитного материала, имеющего на поверхности слой 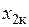 (индекс «к» означает нагретый до температуры выше точки Кюри), у которого
(индекс «к» означает нагретый до температуры выше точки Кюри), у которого 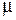 =1, если поверхностный эффект ярко выражен (
=1, если поверхностный эффект ярко выражен (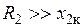 ), могут быть использованы результаты, полученные в работах [1, 3] для полубесконечной среды, на поверхности которой слой глубиной
), могут быть использованы результаты, полученные в работах [1, 3] для полубесконечной среды, на поверхности которой слой глубиной 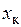 нагрет до температуры выше температуры магнитных превращений (
нагрет до температуры выше температуры магнитных превращений (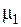 =1).
=1).
При расчете параметров электромагнитного поля в системе индуктор – цилиндр из ферромагнитного материала, имеющий на поверхности слой, нагретый до температуры выше точки Кюри, все параметры для первого слоя цилиндра, где 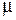 =1, обозначены с индексами «21» (
=1, обозначены с индексами «21» (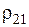 ,
, 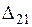 ,
, 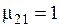 и т.д.), что означает первый слой (индекс «1») цилиндра (индекс «2»), а для второго слоя — с индексами «22» (
и т.д.), что означает первый слой (индекс «1») цилиндра (индекс «2»), а для второго слоя — с индексами «22» (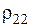 ,
, 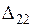 ,
, 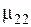 и т.д.), что означает второй слой (индекс «2») цилиндра (индекс «2»).
и т.д.), что означает второй слой (индекс «2») цилиндра (индекс «2»).
Тогда отношения напряженностей магнитного и электрического полей, а также плотности тока в любой точке первой среды к значению этих величин на поверхности цилиндра имеет вид [1, 3]:
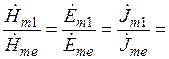
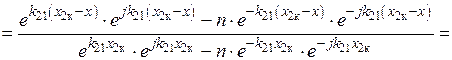
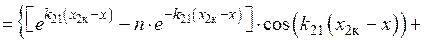
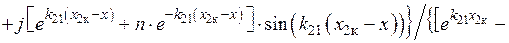
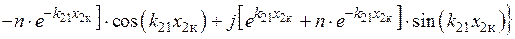 ,
,
где 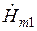 ,
, 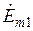 ,
, 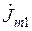 — комплексные значения амплитуд напряженностей магнитного, электрического полей и плотности тока внутри первого слоя глубиной
— комплексные значения амплитуд напряженностей магнитного, электрического полей и плотности тока внутри первого слоя глубиной 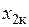 (
(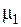 =1) на расстоянии
=1) на расстоянии 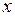 от поверхности цилиндра;
от поверхности цилиндра; 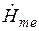 ,
, 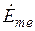 ,
, 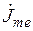 — комплексные значения амплитуд напряженностей магнитного и электрического полей и плотности тока на поверхности цилиндра; параметр
— комплексные значения амплитуд напряженностей магнитного и электрического полей и плотности тока на поверхности цилиндра; параметр 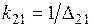 ;
; 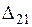 — глубина проникновения тока в материал цилиндра (индекс «2») в первом слое (индекс «1»), т.е. для параметров среды
— глубина проникновения тока в материал цилиндра (индекс «2») в первом слое (индекс «1»), т.е. для параметров среды 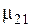 =1 и
=1 и 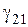 первого слоя (
первого слоя (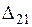 — величина расчетная, чисто условная, т.к. толщина первого слоя
— величина расчетная, чисто условная, т.к. толщина первого слоя 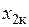 , нагретого до температуры выше температуры магнитных превращений, меньше
, нагретого до температуры выше температуры магнитных превращений, меньше 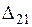 :
: 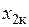 <
< 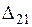 ),
), 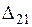 определяется по формуле:
определяется по формуле:
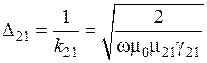 ,
,
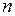 — коэффициент, учитывающий изменение параметров
— коэффициент, учитывающий изменение параметров 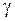 и
и 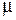 на границе первого и второго слоя; определяется по формуле:
на границе первого и второго слоя; определяется по формуле:
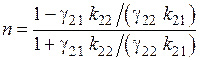 ,
,
где 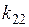 — параметр для второго слоя, определяемый по формуле:
— параметр для второго слоя, определяемый по формуле:
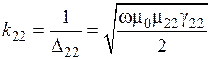 ,
,
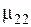 и
и 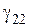 — магнитная проницаемость и электропроводность второго слоя цилиндра.
— магнитная проницаемость и электропроводность второго слоя цилиндра.
После подстановки выражений для 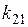 и
и 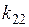 в формулу получаем:
в формулу получаем:
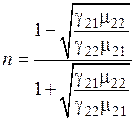 .
.
При 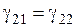 и
и 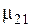 =1 формула упрощается:
=1 формула упрощается:
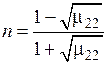 .
.
Из формулы полезно также получить выражение для 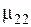 :
:
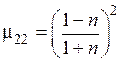 .
.
Модули отношений параметров электромагнитного поля, приведенных в формуле, равны:
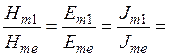
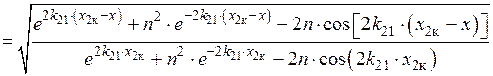 .
.
Распределение напряженностей магнитного и электрического полей, а также плотности тока во втором слое описываются выражениями –.
На рис. 1.5 приведены распределения плотности тока по сечению, которые справедливы для двух сред плоского нагреваемого предмета и цилиндра при ярко выраженном поверхностном эффекте для трех различных глубин нагрева: кривые 1 и 2 для первой среды рассчитаны по формуле, кривая — 3 по формуле без учета влияния второй среды. Распределение тока во второй среде построены по формуле в предположении, что 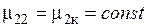 и
и 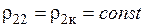 .
.
Из рис. 1.5 видно, что наличие второй среды оказывает значительное влияние на распределение плотности тока в нагреваемом слое (сравн. кривые 1,2 и кривую 3, рассчитанную без учета второй среды).
Влияет наличие второй среды и на полное электрическое сопротивление двухслойной среды. Полное электрическое сопротивление элемента длиной 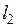 , шириной
, шириной 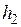 и глубиной много больше
и глубиной много больше 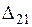 на поверхности двухслойной среды:
на поверхности двухслойной среды:
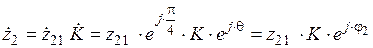 ,
,
где 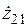 и
и 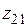 — комплексное значение и модуль полного электрического сопротивления первой среды в предположении, что
— комплексное значение и модуль полного электрического сопротивления первой среды в предположении, что 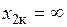 , т.е. первая среда занимает все пространство и вторая среда отсутствует; определяются по формулам:
, т.е. первая среда занимает все пространство и вторая среда отсутствует; определяются по формулам:
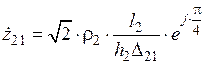 и
и 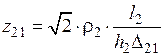 ;
;
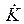 и
и 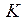 — комплексное значение и модуль параметра, учитывающего влияние второй среды (при
— комплексное значение и модуль параметра, учитывающего влияние второй среды (при 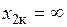
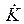 =1);
=1); 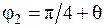 — угол, на который напряженность магнитного поля в первом слое двухслойной среды отстает от напряженности электрического поля (при
— угол, на который напряженность магнитного поля в первом слое двухслойной среды отстает от напряженности электрического поля (при 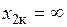
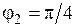 ).
).
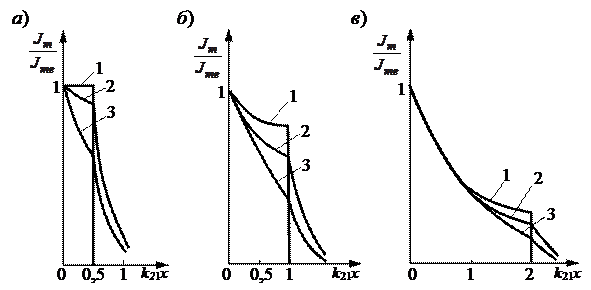
Рис. 1.5. Распределение плотности тока по сечению нагреваемого предмета: а) — 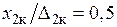 ; б) — ; б) — 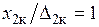 ; в) — ; в) — 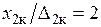 (1 — (1 — 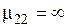 ; 2 — ; 2 — 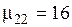 ; 3 — не учтено влияние второй среды, обладающей магнитными свойствами) ; 3 — не учтено влияние второй среды, обладающей магнитными свойствами) |
Параметр 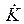 определяется выражением
определяется выражением
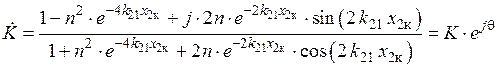
и
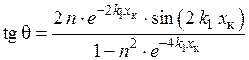 .
.
При 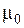 =4p·10–7 Гн/м и
=4p·10–7 Гн/м и 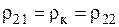 =10–6 Ом·м получим:
=10–6 Ом·м получим:
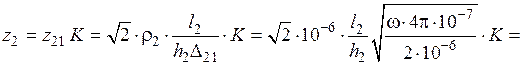
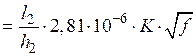 ,
,
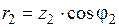 ,
, 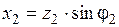 .
.
После этого получим для цилиндра диаметром 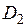 и длиной
и длиной 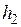 :
:
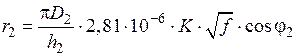 ,
,
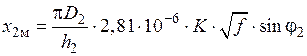 .
.
Для того, чтобы определить параметры 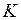 ,
, 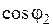 и
и 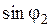 , необходимо определить напряженность магнитного поля на поверхности среды. Воспользуемся формулой и определим удельную мощность, отнесенную к площади поверхности цилиндра.
, необходимо определить напряженность магнитного поля на поверхности среды. Воспользуемся формулой и определим удельную мощность, отнесенную к площади поверхности цилиндра.
Вначале определим мощность, выделяемую в детали. По закону Джоуля–Ленца она равна:
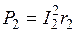 .
.
Ток, протекающий в цилиндре, может быть связан с напряженностью магнитного поля на его поверхности с помощью закона полного тока:
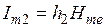 .
.
Тогда:
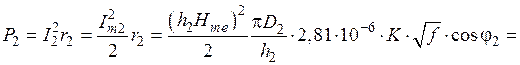
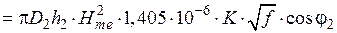 .
.
Тогда удельная мощность, отнесенная к площади поверхности цилиндра, будет равна:
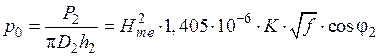 .
.
Отсюда:
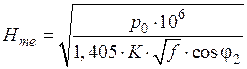 .
.
Затем, задаваясь несколькими значениями 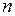 , а значит и
, а значит и 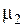 на поверхности второй среды, определяем по табл. П.3–П6 Приложения значения
на поверхности второй среды, определяем по табл. П.3–П6 Приложения значения 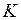 ,
, 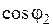 и
и 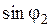 и затем напряженность магнитного поля
и затем напряженность магнитного поля 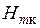 на поверхности второй среды (
на поверхности второй среды (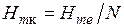 ) и
) и 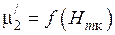 (табл. П.7). Затем на графике
(табл. П.7). Затем на графике 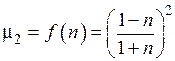 и
и 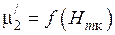 определяем точку, где
определяем точку, где 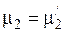 и для определенного значения
и для определенного значения 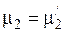 определяем
определяем 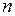 и затем параметры
и затем параметры 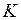 ,
, 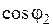 и
и 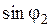 , что позволяет определить активное и реактивное сопротивления ферромагнитного цилиндра, имеющего на поверхности слой глубиной
, что позволяет определить активное и реактивное сопротивления ферромагнитного цилиндра, имеющего на поверхности слой глубиной 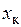 , нагретый до температуры выше температуры магнитных превращений по формулам и.
, нагретый до температуры выше температуры магнитных превращений по формулам и.
Полученное распределение плотности тока для двухслойной среды (рис. 1.5) может быть заменено для теплового расчета более простым — постоянным в слое, глубина которого 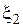 равна:
равна:
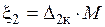 ,
,
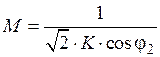 ,
,
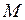 ,
, 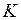 и
и 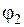 зависят от
зависят от 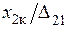 и относительной магнитной проницаемости
и относительной магнитной проницаемости 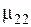 на границе двух сред.
на границе двух сред.
1.2.3. Распределение параметров электромагнитного поля в цилиндре при не ярко выраженном поверхностном эффекте (0,1 R 2 < D2 < 0,4 R 2)
При сквозном нагреве под пластическую деформацию все сечение должно быть прогрето до температуры 900–1250 °С, в связи с чем в конечной стадии нагрева весь металл становится немагнитным.
Для того, чтобы обеспечить равномерный и быстрый нагрев, частоту приходится выбирать таким образом, чтобы горячая глубина проникновения тока 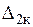 была сравнительно близка к радиусу
была сравнительно близка к радиусу 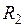 нагреваемого цилиндра. Поэтому при сквозном нагреве поверхностный эффект нельзя считать ярко выраженным, а электромагнитную волну плоской, как это делалось нами при рассмотрении поверхностной закалки.
нагреваемого цилиндра. Поэтому при сквозном нагреве поверхностный эффект нельзя считать ярко выраженным, а электромагнитную волну плоской, как это делалось нами при рассмотрении поверхностной закалки.
В работе [3] (гл. 5, стр. 189–195) рассмотрены электромагнитные процессы и определены распределения напряженностей магнитного (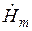 ) и электрического (
) и электрического (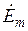 ) поля и плотности тока (
) поля и плотности тока (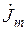 ) в цилиндре при не ярко выраженном поверхностном эффекте. Они имеют следующий вид:
) в цилиндре при не ярко выраженном поверхностном эффекте. Они имеют следующий вид:
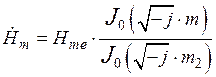 ,
,
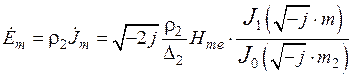 ,
,
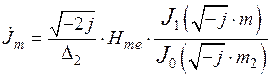 .
.
Так как 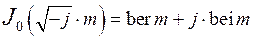 , а
, а 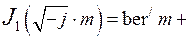
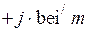 , то выражения – можно представить в виде:
, то выражения – можно представить в виде:
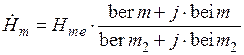 ,
,
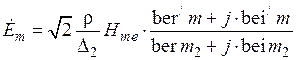 ,
,
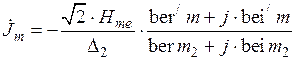 .
.
Здесь 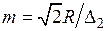 — относительная координата точки в нагреваемом цилиндре, в которой определяются
— относительная координата точки в нагреваемом цилиндре, в которой определяются 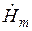 ,
, 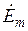 ,
, 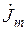 ;
; 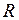 — радиальная координата этой точки (
— радиальная координата этой точки (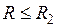 );
); 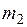 — относительная координата точки на поверхности цилиндра (
— относительная координата точки на поверхности цилиндра (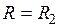 ), определяется по формуле:
), определяется по формуле:
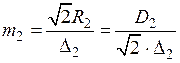 ,
,
 |
| Рис. 1.6. Распределение плотности тока по сечению металлического цилиндра |
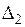 — глубина проникновения тока в полуограниченное металлическое тело с плоской поверхностью или в материал цилиндра при ярко выраженном поверхностном эффекте
— глубина проникновения тока в полуограниченное металлическое тело с плоской поверхностью или в материал цилиндра при ярко выраженном поверхностном эффекте 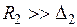 );
); 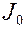 и
и 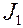 — символы функций Бесселя первого рода нулевого и первого порядков.
— символы функций Бесселя первого рода нулевого и первого порядков.
Функции 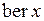 ,
, 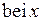 ,
, 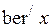 ,
, 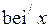 позволяют разделить вещественные и мнимые величины комплексных функций
позволяют разделить вещественные и мнимые величины комплексных функций 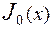 и
и 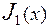 .
.
На рис. 1.6 приведено распределение плотности тока по сечению цилиндра при различных значениях 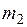 . Из кривых видно, что уже при
. Из кривых видно, что уже при 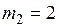 , что соответствует
, что соответствует 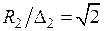 , зависимость
, зависимость 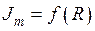 близка к линейной. При этом и напряженность магнитного поля почти постоянна.
близка к линейной. При этом и напряженность магнитного поля почти постоянна.
При 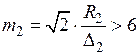 (высокая частота):
(высокая частота):
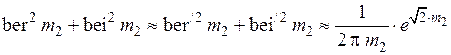 .
.
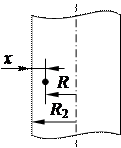 |
| Рис. 1.7. Обозначения радиальных координат |
Тогда при 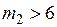 (
(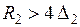 ), учитывая, что
), учитывая, что 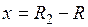 (рис. 1.7), получаем:
(рис. 1.7), получаем:
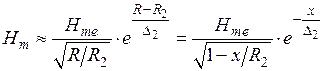 ,
,
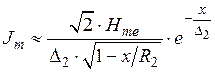 .
.
При 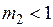 , т.е. при
, т.е. при 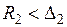 (низкая частота):
(низкая частота):
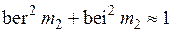 и
и 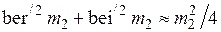 .
.
Тогда: 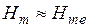 и
и
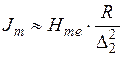 .
.
Таким образом, для 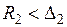 напряженность магнитного поля приблизительно постоянна по всему сечению, а плотность тока уменьшается от
напряженность магнитного поля приблизительно постоянна по всему сечению, а плотность тока уменьшается от 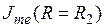 до нуля при R = 0 по линейному закону.
до нуля при R = 0 по линейному закону.
Ток, наведенный в металлическом цилиндре, нагревает его. Распределение температуры в цилиндре зависит от распределения плотности тока, т.е. от распределения в цилиндре источников тепла.
Электрическое сопротивление цилиндра диаметром 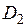 и длиной
и длиной 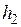 (при
(при 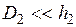 ) равно [1, 3]:
) равно [1, 3]:
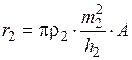 ,
,
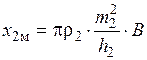 ,
,
где 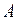 — коэффициент, учитывающий изменение активного сопротивления цилиндра при не ярко выраженном поверхностном эффекте; определяется по формуле:
— коэффициент, учитывающий изменение активного сопротивления цилиндра при не ярко выраженном поверхностном эффекте; определяется по формуле:
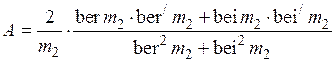 ,
,
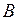 — коэффициент, учитывающий изменение внутреннего индуктивного сопротивления цилиндра при не ярко выраженном поверхностном эффекте; определяется по формуле:
— коэффициент, учитывающий изменение внутреннего индуктивного сопротивления цилиндра при не ярко выраженном поверхностном эффекте; определяется по формуле:
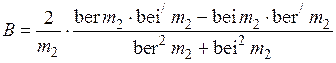 .
.
Выражения и можно записать в более удобном виде:
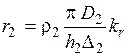 ,
,
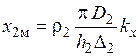 ,
,
где 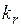 и
и 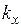 — коэффициенты, учитывающие степень проявления поверхностного эффекта (при ярко выраженном поверхностном эффекте
— коэффициенты, учитывающие степень проявления поверхностного эффекта (при ярко выраженном поверхностном эффекте 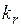 и
и 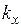 равны 1), они определяются по формулам:
равны 1), они определяются по формулам:
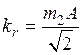 ,
, 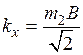 .
.
Значения коэффициентов 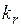 и
и 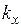 приведены в табл. П.9.
приведены в табл. П.9.
 2015-04-01
2015-04-01 976
976








