2015-04-01
3567
Предположим, что n = 2 m, где n – общее число отрезков разбиения промежутка [ a, b ]. Затем на каждом отрезке [ xk, xk + 2], k = 0, 2, 4, …, 2 m – 2 аппроксимируем кривую y = f (x) параболической кривой zk = akx 2 + bkx + ck, где коэффициенты ak, bk и ck определены таким образом, чтобы кривая zk проходила через точки (xk, f (xk)), (xk + 1, f (xk + 1)) и (xk + 2, f (xk + 2)). Очевидно, что исходя из этих условий коэффициенты ak, bk и ck определяются однозначно.
Заменим далее площадь под кривой y = f (x) на каждом отрезке
[ xk, xk + 2], k = 0, 2, 4, …, 2 m – 2 площадью параболической трапеции, ограниченной сверху определенной по правилу параболической кривой
zk = akx 2 + bkx + ck. Такая замена приведет к квадратурной формуле Симпсона (ее называют также квадратурной формулой параболических трапеций) на каждом отрезке [ xk, xk + 2 ]:
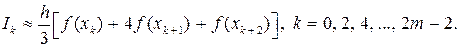(4.3.23)
Составная квадратурная формула Симпсона (параболических трапеций) для отрезка [ a, b ] имеет вид
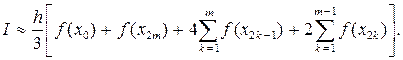(4.3.24)
Для квадратурной формулы Симпсона (4.3.23) оценка погрешности аппроксимации определяется неравенством
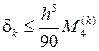, (4.3.25)
где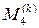 
– максимум модуля четвертой производной функции f (x) на отрезке [ xk, xk + 2], k = 0, 2, 1, …, 2 m – 2.
Для составной квадратурной формулы Симпсона (4.3.24)
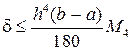, (4.3.26)
где M 4 – максимум модуля четвертой производной функции f (x) на отрезке [ a, b ].
Таким образом, квадратурная формула Симпсона (4.3.23) имеет пятый, а составная квадратурная формула (4.3.24) – четвертый порядок точности по h. Из оценок (4.3.25) и (4.3.26) следует также, что квадратурная формула Симпсона (4.3.23) точна для полиномов до третьего порядка включительно.
Организация расчетов по рассмотренным квадратурным формулам предельно проста, поскольку сводится к суммированию с весовыми коэффициентами значений интегрируемой функции в узлах той или иной квадратурной формулы. Например, при использовании составной формулы Симпсона (4.3.24) данные удобно представить в виде таблицы, аналогичной табл. 4.3.1 (n = 2m – общее число отрезков разбиения отрезка интегрирования [ a, b ] должно быть четным).
Таблица 4.3.1
| Номер узла | xi | f (xi), i = 0, 2 m | f (xi), i = 2k – 1, k = 1, 2, …, m | f (xi), i = 2 k, k = 1, 2,..., m – 1 |
| x 0 | f (x 0) | |||
| x 1 | f(x1) | |||
| x 2 | f (x 2) | |||
| x 3 | f(x3) | |||
| x 4 | f (x 4) | |||
| x 5 | f(x5) | |||
| x 6 | f (x 6) | |||
| x 7 | f(x7) | |||
| x 8 | f (x 8) | |||
| x 9 | f(x9) | |||
| x 10 | f (x 10) | |||
| ∑ | (1) | (2) | (3) | |
| I» h [(1) + 4(2) + 2(3)]/3 |
В заключение дадим общую характеристику рассмотренных квадратурных формул.
1. Квадратурные формулы левых и правых прямоугольников редко применяются в реальных расчетах ввиду их невысокой точности. В практическом отношении наибольшую ценность имеет часто используемая квадратурная формула Симпсона.
2. Выбор наилучшего распределения узлов на отрезке интегрирования является дополнительной возможностью для повышения точности квадратурных формул. Эта возможность реализована в квадратурных формулах Гаусса, имеющих наивысшую алгебраическую точность.
3. Исходя из приведенных выше оценок погрешностей аппроксимации, нельзя вычислить действительную точность приближенного значения определенного интеграла, найденного с помощью квадратурных формул. Это объясняется невозможностью с достаточной степенью точности оценить значение максимума модуля производной интегрируемой функции на отрезке [ a, b ]. Рассматриваемое в п. 4.3.2 правило Рунге позволяет обойти эту проблему при оценке точности численного интегрирования.
