Основные понятия. В данном параграфе рассматриваются численные методы решения задачи Коши для обыкновенного дифференциального уравнения первого порядка и систем

В данном параграфе рассматриваются численные методы решения задачи Коши для обыкновенного дифференциального уравнения первого порядка и систем дифференциальных уравнений первого порядка.

Задача Коши для системы дифференциальных уравнений первого порядка формулируется следующим образом: найти функции yk = fk (x), k = 1, 2, …, n, удовлетворяющие системе дифференциальных уравнений 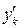= gk (x, y 1, y 2, …, yn), k = 1, 2, …, n (5.1.1) и начальным условиям yk (x 0) = y 0( k ), k = 1, 2, …, n, (5.1.2) где y 0( k ), k = 1, 2, …, n – заданные числа.

Более подробно эту задачу можно сформулировать так: найти функции y_k = f_k (x), k = 1, 2, …, n, удовлетворяющие системе дифференциальных уравнений

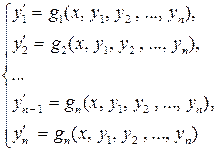(5.1.3)

и начальным условиям

y ₁(x ₀) = y ₍₁₎₀, y ₂(x ₀) = y ₍₂₎₀, …, y_{n – 1}(x ₀) = y _{( n – 1)0}, y_n (x ₀) = y _{( n )0}, (5.1.4)

где y _(1)0, y ₍₂₎₀, …, y _{( n – 1)0,} y _{( n )0} – заданные числа.

В дальнейшем предполагается, что условия теоремы существования и единственности для задачи (5.1.3), (5.1.4) выполнены.

Положим a:= x ₀ и будем искать решение задачи Коши (5.1.3), (5.1.4) на отрезке [ a, b ]. При построении численного решения получим приближенное решение задачи

j_{(1) h} (x)» f ₁(x); j_{(2) h} (x)» f ₂(x);…;j_{(n – 1) h} (x)» f_{n – 1}(x); j_{(n) h} (x)» f_n (x), (5.1.5)

которое представлено значениями функций j_{(k) h} (x), k = 1, 2, …, n в узлах заданной на отрезке [ a, b ] одномерной сетки

h _x = { x_i / x_i = x_{i – 1} + h_i, h_i > 0, i = 1, 2, 3, …, m; x ₀ = a, x_m = b }, (5.1.6)

где x_i, i = 0, 1, 2, …, m – узлы одномерной сетки; h_i, i = 1, 2, 3, …, m – ее шаг.

Для простоты будем полагать, что сетка h _x равномерная:
h_i = h, i = 1, 2, 3, …, m. Таким образом, в результате численного решения задачи (5.1.3) - (5.1.4) получим значения j_{(k) h} (x ₀), j_{(k) h} (x ₁), j_{(k) h} (x ₂), …, j_{(k) h} (x_n) функций j_{(k) h} (x), k = 1, 2, …, n. Эти результаты удобно представлять в табличной форме (табл. 5.1.1).

Таблица 5.1.1

Номер узла	Узлы сетки	j(1) h (x)» » f 1(x)	j(2) h (x)» » f 2(x)	j(3) h (x)» » f 3(x)	…	j(n – 1) h (x)» » fn – 1(x)	j(n) h (x)» » fn (x)
	x 0	j(1) h (x 0)	j(2) h (x 0)	j(3) h (x 0)	…	j(n -- 1) h (x 0)	j(n) h (x 0)
	x 1	j(1) h (x 1)	j(2) h (x 1)	j(3) h (x 1)	…	j(n -- 1) h (x 1)	j(n) h (x 1)
	x 2	j(1) h (x 2)	j(2) h (x 2)	j(3) h (x 2)	…	j(n -- 1) h (x 2)	j(n) h (x 2)
….	…	…	…	…	...	…	…
m – 1	xm – 1	j(1) h (xm – 1)	j(2) h (xm – 1)	j(3) h (xm -- 1)	…	j(n – 1) h (xm – 1)	j(n) h (xm – 1)
m	xm	j(1) h (xm)	j(2) h (xm)	j(3) h (xm)	…	j(n – 1) h (xm)	j(n) h (xm)

Как известно, к задаче (5.1.3) - (5.1.4) сводится и задача Коши для обыкновенного дифференциального уравнения n -го порядка:

найти функцию y = f (x), удовлетворяющую дифференциальному уравнению

y ⁽ⁿ⁾ = g (x, y, y ^¢, y ⁽²⁾, …, y ^{(n – 2)}, y ^{(n – 1)}) (5.1.7)

и начальным условиям

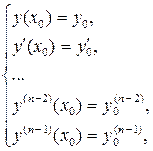(5.1.8)

где 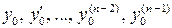– заданные числа (здесь y ^{( k )} - производная k -го порядка функции y = f (x)).

Сведение задачи (5.1.7) - (5.1.8) к решению системы дифференциальных уравнений вида (5.1.3), (5.1.4) осуществляется посредством переобозначения:

y ₁:= y ^¢; y ₂:= y ⁽²⁾;…; y_{n – 1}:= y ^{(n – 1)}; y_n: = y ⁽ⁿ⁾. (5.1.9)

В результате вместо дифференциального уравнения n -го порядка (5.1.7) может быть записана система n дифференциальных уравнений первого порядка

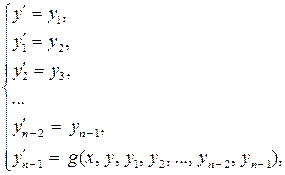(5.1.10)

а начальные условия (5.1.8) переписываются в обозначениях (5.1.9), что приводит к задаче вида (5.1.3), (5.1.4).

Как частный случай (n = 1) задачи (5.1.3), (5.1.4) запишем задачу Коши для дифференциального уравнения первого порядка, которая может быть сформулирована следующим образом:

найти функцию y = f (x), удовлетворяющую дифференциальному уравнению

y ¢ = g (x, y) (5.1.11)

и начальному условию

y (x ₀) = y ₀, (5.1.12)

где y ₀ – заданное число.

Предположим, как и ранее, что условия теоремы существования
и единственности решения задачи (5.1.11), (5.1.12) выполнены. Положим a:= x ₀ и будем искать решение задачи Коши (5.1.11), (5.1.12) на отрез-
ке [ a, b ]. В результате численного решения поставленной задачи получим приближенное решение

j _h (x)» f (x), (5.1.13)

которое представлено значениями j _h (x) в узлах заданной на отрезке [ a, b ] одномерной равномерной сетки h _x (5.1.6) с шагом h.

Таким образом, в результате численного решения задачи (5.1.11), (5.1.12) получаем значения j _h (x ₀), j _h (x ₁), j _h (x ₂), …, j _h (x_m) функции j _h (x) – приближенное решение задачи.

В последующих параграфах данной главы будут рассмотрены конкретные численные методы решения применительно к задаче (5.1.11), (5.1.12) – задаче Коши для одного обыкновенного дифференциального уравнения первого порядка. Вместе с тем рассматриваемые методы могут применяться и для решения задачи Коши для системы дифференциальных уравнений первого порядка (5.1.3), (5.1.4).

Рассматриваемые численные методы решения задачи Коши (5.1.11), (5.1.12) можно разделить на две группы:

– многошаговые разностные методы. К ним относятся метод Эйлера (§ 5.2) и явный 4-шаговый метод Адамса (§ 5.3);

– методы Рунге – Кутта (в § 5.4 будет рассмотрен метод Рунге – Кутта четвертого порядка).

Эти методы имеют некоторые общие свойства и характеристики.

Как следует из вышесказанного, j _h (x) – приближенное решение, полученное в результате численного решения задачи Коши, представлено значениями в узлах одномерной равномерной сетки h _x с шагом h - j _h (x ₀), j _h (x ₁),j _h (x ₂), …, j _h (x_m). Расчет значений приближенного решения j _h (x) в узлах сетки осуществляется для всех рассматриваемых численных методов решения задачи Коши по правилу

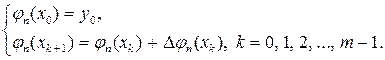(5.1.14)

Таким образом, отличие одного численного метода от другого заключается лишь в способе построения Dj _h (x_k), k = 0, 1, 2, …, m – 1.

Важными характеристиками численного метода являются также оценки погрешности и сходимость. Погрешность метода часто оценивают с помощью так называемого порядка точности метода.