Основные понятия линейного программирования

Определение. Общей задачей линейного программирования называется задача, которая состоит в определении максимума (минимума) целевой функции

Z(x₁,...x_n) = c₁x₁+...+c_nx_n 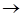max (min) (2. 1)

при ограничениях:

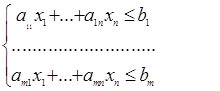(2.2)

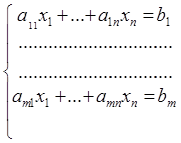(2.3)

x _j 0, (j = 1,….n). (2.4)

Определение. Функция (2.1) называется целевой функцией или линейной формой задачи линейного программирования, а условия (2.2) - (2.4) - ограничениями данной задачи.

Определение. Стандартной (симметричной) задачей линейного программирования называется задача, которая состоит в определении экстремального значения целевой функции (2.1) при выполнении условий (2.2) и (2.4).

Определение. Основной (канонической) задачей линейного программирования называется задача, которая состоит в определении экстремального значения целевой функции (2.1) при выполнении условий (2.3) и (2.4).

Определение. Вектор или совокупность чисел `Х = (х₁, х₂,...., х_n), удовлетворяющих ограничениям задачи (2.2) - (2.4), называется допустимым решением или планом задачи линейного программирования.

Определение. План `Х*=(х₁^*, х₂^*,...., х_n^*), при котором целевая функция (2.1) принимает свое оптимальное (минимальное или максимальное) значение, называется оптимальным планом.

Таким образом, линейное программирование является частью математического программирования, особенностью которого является то, что исследуемая целевая функция является линейной: Z(x₁,...,x_n)=c₁x₁+...+c_nx_n, а ограничения, накладываемые на переменные, представляют собой линейные уравнения или неравенства.

Если же целевая функция или система ограничений нелинейная, то соответствующая задача является задачей нелинейного программирования.

Если требуется провести поиск целочисленных значений x _j, то приходим к задаче целочисленного линейного программирования (ЦЛП).

2.2. Геометрическое решение задач линейного программирования

Геометрическое решение задач линейного программирования приемлемо для случаев n 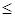3.

Как известно, линейное уравнение a₁x₁ + a₂x₂ = b задает на плоскости (в пространстве R²) прямую; уравнение a₁x₁ + a₂x₂ + a₃x₃ = b - плоскость в R³. Точно так же уравнение a_i1x₁ +... + a_inx_n= b_i (i - е ограничение в канонической задаче ЛП) определяет в пространстве Rⁿ некоторое множество, называемое гиперплоскостью.

Определение. Фигура на плоскости называется выпуклой, если наряду с любыми ее точками М₁ и М₂ ей принадлежат и все точки отрезка М₁М₂.

Например, отрезок, треугольник, квадрат, острый угол.

Определение. Множество X называется выпуклым, если вместе с любыми двумя точками (элементами) (x, y); (x, y) 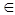X оно содержит отрезок между этими точками, т.е. точки вида

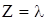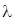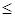
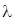
y+( 1 - )x, (0 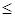1).

Это уравнение является уравнением отрезка.

Теорема. Пересечение любого числа выпуклых множеств является выпуклым множеством.

Очевидно, прямая в R², плоскость в R³ являются выпуклыми множествами. Точно так же, выпуклым множеством является гиперплоскость a_i1x₁ +... + a_inx_n = b_i и полупространство (вместе с границей) в Rⁿ, определяемое i -м ограничением в стандартной задаче:

a_i1x₁ +... + a_inx_n 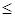b_i.

Система ограничений (2.2) задает множество М - пересечение m выпуклых множеств в n -мерном евклидовом пространстве Rⁿ, поэтому само является выпуклым множеством. Множество М называется выпуклым многогранником (областью) допустимых решений.

При наличии только двух переменных М задает многоугольник решений в R², а в случае переменных x₁, x₂, x₃ - выпуклый многогранник в пространстве R³.

Геометрическое решение задачи линейного программирования состоит в том, что из всех допустимых решений требуется выделить оптимальное решение, определяющее экстремум целевой функции Z.

Теорема. Функция цели (2.1) задачи линейного программирования достигает экстремума в угловой точке выпуклого множества допустимых решений.

Решить задачу графического - значит найти угловую точку выпуклого множества области допустимых решений, координаты которой дают экстремум функции цели.