Новые представления о форме реальных объектов природы, о структурах в биологии и материаловедении основаны на понятии фракталов, которое впервые сформулировал в 1977г. Бенуа Мандельброт / Б.Мадельброт Фрактальная геометрия природы. М. 20002г/ В 1984 г. он сказал: «Почему геометрию часто называют холодной и сухой? Одна из причин заключается в её неспособности описать форму облака, горы, берега моря и т.п. Облака – это не сферы, горы – это не конусы, линии берега – это не окружности и кора не является гладкой, и молния не распространяется по прямой… Природа демонстрирует нам не просто более высокую степень, а совсем другой уровень сложности. Число различных масштабов длин в структурах всегда бесконечно».
Мандельброт ввел понятие не только фрактала, но и фрактальной геометрии, отличающейся от Евклидовой дробными размерностями, и обратил внимание на то, что контуры поверхности и объемы окружающих нас предметов не так ровны, гладки и совершенны, как принято думать. В действительности они неровны, шершавы, изъязвлены множеством отверстий самой причудливой формы, пронизаны трещинами, порами, покрыты морщинами, царапинами и т.п.
Для количественной оценки этих отклонений от идеальности Мандельброт применил удобные размерности, описанные ранее в математике Хаусдорфом - Безековичем. Применительно к идеальным объектам Евклидовой геометрии эта новая количественная оценка давала те же численные значения, что и известная топологическая размерность, т.е.
0 - для точки;
1 - для плавной линии;
2 - для фигуры и поверхности;
3 – для тела и пространства.
| 3 - объем зерна, субзерен, блоков, фрагментов (напр. алмаз) | 2 – поверхность высотой 1-100 нм (поверхностные дефекты, границы зерен) | 1 – линия дислокации | 0 – вакансии и другие точечные дефекты. |
 |  |    |  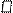  |
Но в случае оценки морфологии[1] реальных структур новая размерность обладала более тонкой чувствительностью ко всякого рода несовершенствам реальных объектов. Так отрезки прямой, синусоиды и самый сложный меандр[2] неразличимы при использовании топологической[3] размерности. Все они имею топологическую размерность, равную 1. Но по шкале Хаусдорфа – Безековича они различаются и числом можно измерить степень их извилистости. Размерность Хаусдорфа – Безековича увеличивается по мере возрастания извилистости линии или шероховатости поверхности. Это изменение не сопровождается скачками как в топологии, а плавно меняется по мере возрастания дефектности.
Так возникло понятие фракталы – объекта с дробной (фрактальной) размерностью. Для физиков – это объекты, характеризующиеся самоподобием в широком интервале масштабов рассмотрения или измерения.Материаловед видит во фрактальности возможность количественной оценки реальной структуры материалов.
Примеры природных фракталов – поверхности разлома горных пород и металлов, облака, пена, частицы сажи и т.п. Они лишены явного геометрического подобия, но упорно воспроизводят в каждом фрагменте статистические свойства целого. Пример искусственного фрактала на рисунке 1– «ковер Серпинского» (мозаика на полу церкви в городе Ананьи в Италии).
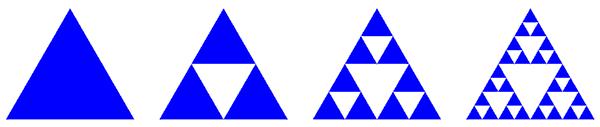 | |||
| Lо=20(=1) Мо=30 (=1) | L1=21 М1=31 | L2=22 М2=32 | L3=23 М3=33 |

Фото ковер Серпинского 6-го поколения, полученный травлением ионным пучком поверхности монокристаллического кремния / https://www.nanometer.ru/2010/06/19/fraktali_fib_214547.html/.
Рис. 1. - ковер Серпинского.
Фрактальная размерность как зависимость массы объекта от его размера.
Процесс можно продолжать до бесконечности, но важно: (рис. 2- зависимость lg M(lgL))
tg α = lg3/lg2=1,58 – D –фрактальная размерность для ковра Серпинского.
Физический смысл «ковра Серпинского» состоит в том, что ковер заполняет пространство плотнее, чем совокупность отрезков, имеющих размерность D=1, но менее плотно, чем целый треугольник D=2.
Снежинка «фон Коха» тоже является самоподобным объектом. Кристалл льда – типичный самоподобный фрактал, как и дендрит, образуется при первичной кристаллизации. Чтобы их описать в рамках евклидовой геометрии, нужно знать положение каждой её точки в пространстве. С помощью фрактальной геометрии потребуется знать всего лишь 3 параметра: D, Rmin, Rmах. D=1,71.
Существуют помимо ковра Серпинского, снежинки Коха и др. идеально самоподобные (регулярные) фракталы: губка Менгера, Вселенная Фурье. Для большинства из них фрактальная размерность может быть вычислена аналитически. В любом масштабе фрактал выглядит одинаково, т.е. составляющие части фрактала подобны целому.
Образование фракталов изучают многие науки. Среди них и материаловедение. Центральный вопрос материаловедения – изучение структуры материалов и установление связи между структурными параметрами и свойствами.
Традиционно анализ структуры на различных (макро- и микро-) уровнях проводят путем количественных замеров структурных составляющих с помощью топологических размерностей. При этом допускают значительные условные приближения очень сложных реальных структур к простым фигурам евклидовой геометрии.
Фрактальная геометрия позволяет описывать структуры любой сложности, содержащей большое количество дефектов – пористые структуры, шероховатые поверхности, сложные контуры избыточных фаз, структуры сетки трещин, поверхности разрушений. Проявляемый в них признак самоподобия, количественно выражается с помощью понятия фрактальной размерности D.
Так, если некоторую структуру можно разбить на N подобных друг другу и самой структуре частей (структурных единиц) в 1/ε (ε<1) меньшего размера, и с каждой структурной единицей на любом масштабе можно сделать то же самое, то размерность такой структуры вычисляется по формуле:
D=lgN/lg(1/ε),
что подразумевает степенную зависимость N~ε-D (скейлинг). Например, при больших и малых увеличениях материал выглядит одинаково пористым. При этом зависимость объемной плотности пор от их линейного размера является степенной.
В случае обычных плотных структур (отрезка, квадрата, куба, сферы и т.д.) эта формула дает целые значения и фрактальная размерность D=De (евклидовой размерности): для линии D=De=1;
для квадрата D=De =2;
для куба D=De=3.
 2015-04-01
2015-04-01 2002
2002
