Метод контурных токов

Метод позволяет уменьшить число совместно решаемых уравнений по сравнению с числом уравнений, составляемых по законам Кирхгофа.

Рассмотрим электрическую цепь (рис.1.18), в которой выберем три независимых контура. Контуры образованы собственными контурными ветвями и общими ветвями контуров. Направления токов и ЭДС в ветвях указаны произвольно, кроме того, заданы параметры сопротивлений и ЭДС в ветвях. Необходимо определить токи ветвей. В независимых контурах произвольно выберем направления контурных токов и ЭДС, которые обозначим по номеру контура с одинаковыми двойными индексами номеров контуров.

Пусть направления контурных токов и ЭДС совпадают с направлениями токов и ЭДС собственных контурных ветвей и значения этих токов равны, т.е.

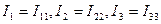
Токи в общих ветвях контуров определяются по первому закону Кирхгофа:

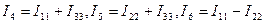
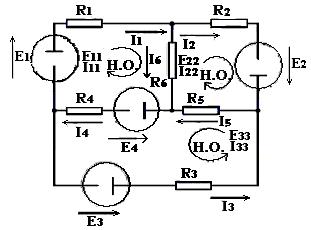
Рис.1.18. Электрическая схема с тремя независимыми контурами

Контурные ЭДС равны алгебраической сумме ЭДС ветвей, входящих в каждый независимый контур:

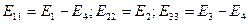
Арифметические суммы сопротивлений всех резистивных элементов, входящих в каждый из выбранных контуров, называются собственными контурными сопротивлениями, и обозначаются двойными индексами номеров контуров:

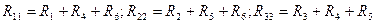
Сопротивления резистивных элементов, находящихся в общих ветвях двух контуров, называются общими сопротивлениями этих контуров:

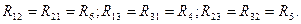
Для определения контурных токов составим систему контурных уравнений по второму закону Кирхгофа для рассматриваемой электрической цепи, у которой три независимых контура:

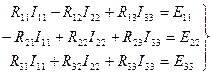(1.54)

Подставим в значения собственных и контурных сопротивлений резистивных элементов ветвей, а также в значения контурных ЭДС ветвей цепи, систему уравнений (1.54) преобразуем:

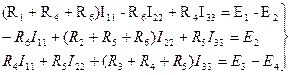(1.55)

Систему уравнений (1.55) представим в матричной форме

AI = E, (1.56)

где А - квадратная матрица 3х3 постоянных коэффициентов значений сопротивлений при контурных токах цепи, I - вектор-столбец неизвестных контурных токов, Е - вектор-столбец постоянных коэффициентов значений контурных ЭДС цепи.

Преобразуем систему уравнений (1.56)

I = A ֿ ¹E. (1.57)

Система уравнений (1.57) в раскрытой матричной форме будет иметь вид:

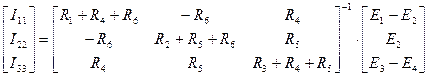
В среде MATLAB выражение (1.57) будет иметь вид:

I = inv (A)*E, (1.58)

где inv(A) - инверсия матрицы А; E - вектор - столбец значений ЭДС цепи.

После подстановки значений сопротивлений и ЭДС ветвей цепи, компьютер выдаст численное решение неизвестных значений контурных токов цепи: 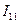, , 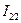, 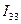по которым легко определяются значения токов ветвей цепи.