Проанализируем процессы в цепи переменного тока, представленной на рис.2.18.
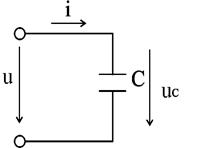
Рис.2.18. Цепь переменного тока с ёмкостью
Зададимся напряжением на зажимах источника 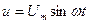 , тогда ток в цепи с ёмкостью так же будет меняться по синусоидальному закону. Ток определяется по формуле
, тогда ток в цепи с ёмкостью так же будет меняться по синусоидальному закону. Ток определяется по формуле 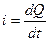 . Количество электричества Q конденсатора связано с напряжением на ёмкости и его ёмкостью:
. Количество электричества Q конденсатора связано с напряжением на ёмкости и его ёмкостью: 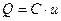 . Следовательно,
. Следовательно,
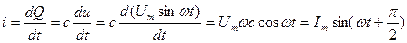 (2.16)
(2.16)
Таким образом, ток в цепи с ёмкостью опережает по фазе напряжение на угол 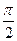 (рис. 2.19).
(рис. 2.19).
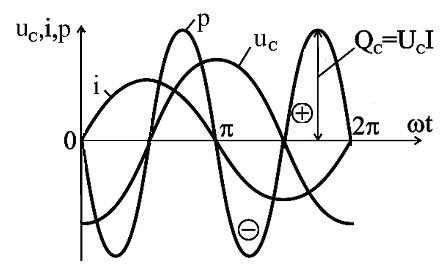
Рис.2.19. Зависимости мгновенных значений напряжения, тока и мощности цепи переменного тока с ёмкостью
Сопоставляя значения для мгновенного тока и напряжения в цепи с ёмкостью, имеем: 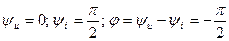 . Из формулы (2.16) выведем закон Ома для амплитудных значений:
. Из формулы (2.16) выведем закон Ома для амплитудных значений: 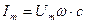 или
или
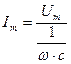 . (2.17)
. (2.17)
Введем обозначение: 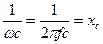 , где
, где 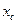 - емкостное сопротивление. Действительно, если
- емкостное сопротивление. Действительно, если 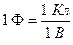 , то
, то 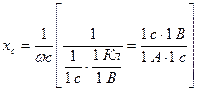 измеряется в Омах.
измеряется в Омах.
Закон Ома для действующих значений напряжения 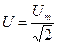 и тока
и тока 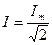 имеет выражение:
имеет выражение:
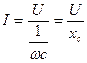 . (2.18)
. (2.18)
Для комплексных чисел закон Ома записывается в виде
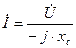 . (2.19)
. (2.19)
Диаграммы в векторном и комплексном видах представлены на рис. 2.20.
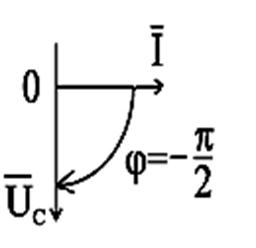
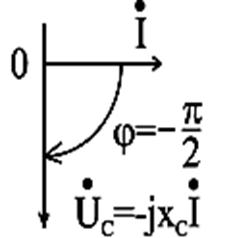
Рис.2.20. Векторные диаграммы действующих значений тока и напряжения цепи переменного тока с ёмкостью в векторном и комплексном виде
Так как напряжение на ёмкости отстает от тока на угол 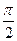 , который изменяется по косинусоиде, то мгновенную мощность выразим в виде:
, который изменяется по косинусоиде, то мгновенную мощность выразим в виде:
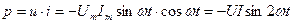 , (2.20)
, (2.20)
где 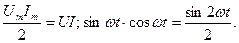
Мгновенная мощность p имеет частоту 2ω, но в отличие от индуктивности, здесь мощность положительна, пока возрастает напряжение на ёмкости. Происходит накопление энергии электрического поля на конденсаторе. Затем конденсатор разряжается на источник, и мощность становится отрицательной.
Из рис. 2.19 видно, что средняя или активная мощность P = Pср= 0. Амплитуда колебаний мощности в цепи с ёмкостью называют реактивной емкостной мощностью:
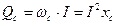 . (2.21)
. (2.21)
Единицей реактивной емкостной мощности является вольт-ампер реактивный (вар).
 2015-04-01
2015-04-01 2714
2714








