Определение производной. Пусть задана однозначная функция на области D (открытом связном множестве) комплексной плоскости

Пусть задана однозначная функция 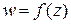на области D (открытом связном множестве) комплексной плоскости.

Определение. Производной функции 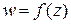в точке z называется предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю

.

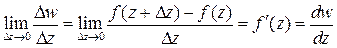Если этот предел существует, то функция 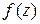называется дифференцируемой в точке .

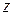Если функция 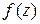является дифференцируемой в каждой точке области 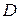, то говорят, что она аналитическая в области .

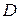Поскольку определение производной функции комплексного переменного полностью аналогично определению производной функции действительной переменной, то в случае дифференцируемости функции 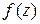, все известные правила дифференцирования остаются в силе.