Теорема 1 (Условия Коши – Римана). Для того, чтобы функция 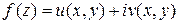 , определенная в некоторой области
, определенная в некоторой области 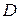 , была дифференцируема в точке
, была дифференцируема в точке 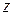 этой области, как функция комплексного переменного, необходимо и достаточно, чтобы функции
этой области, как функция комплексного переменного, необходимо и достаточно, чтобы функции 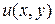 и
и 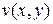 были дифференцируемы в той же точке (как функции действительных переменных) и, чтобы, кроме того, выполнялись условия:
были дифференцируемы в той же точке (как функции действительных переменных) и, чтобы, кроме того, выполнялись условия:
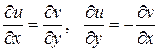 .
.
При выполнении условий теоремы, производная функции 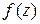 может быть представлена в виде:
может быть представлена в виде:
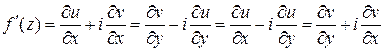 .
.
 2015-04-01
2015-04-01 3312
3312
