Свойства модуля и аргумента комплексного числа позволяют получить формулу возведения комплексного числа в целую положительную степень:

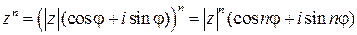 - эту формулу называют формулой Муавра.
- эту формулу называют формулой Муавра.
Или в показательной форме 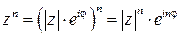 .
.
Легко проверить, что эта формула остается справедливой и для 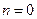 , и для целых отрицательных степеней.
, и для целых отрицательных степеней.
Пример. Найти 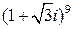
Решение. Запишем сначала число 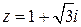 в тригонометрической форме:
в тригонометрической форме:
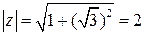 ,
, 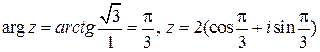 .
.
По формуле Муавра имеем:
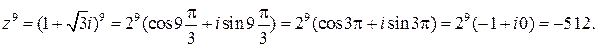 Определение. Корнем n-ой степени из комплексного числа
Определение. Корнем n-ой степени из комплексного числа 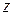 называется такое комплексное число
называется такое комплексное число 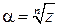 , для которого:
, для которого: 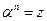 .
.
Из определения и формулы Муавра ясно, что модуль искомого корня будет 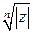 , а аргумент
, а аргумент 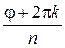 , где
, где 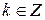 . Таким образом,
. Таким образом,
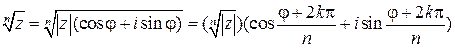
или 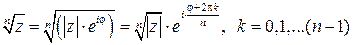 .
.
Придавать «k» значения, большие, чем 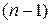 не имеет смысла, так как будем получать уже имеющиеся значения аргумента (с точностью до
не имеет смысла, так как будем получать уже имеющиеся значения аргумента (с точностью до 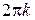 ). Следовательно, корень n-ой степени из комплексного числа имеет n различных значений, модули которых одинаковы (
). Следовательно, корень n-ой степени из комплексного числа имеет n различных значений, модули которых одинаковы (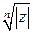 ), а аргументы двух последовательных значений отличаются на угол
), а аргументы двух последовательных значений отличаются на угол 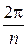 . Таким образом, все значения корня лежат на окружности с центром в начале координат радиуса
. Таким образом, все значения корня лежат на окружности с центром в начале координат радиуса 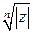 .
.
Пример. Вычислить все значения корня 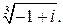
Решение. 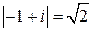 ,
, 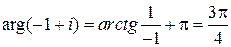 ,
, 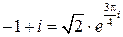 ,
,
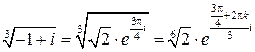 ,
, 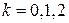 .
.
Ответ. 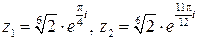 ,
, 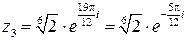 .
.
Пример. Найти все значения 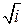 .
.
Решение. Имеем 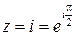 , тогда
, тогда 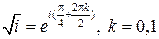 .
.
Ответ. 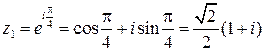 ,
, 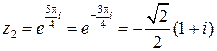 .
.
1.2. Функции комплексного переменного
Пусть 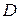 - некоторое множество комплексных чисел (или множество точек комплексной плоскости). Пусть комплексное число
- некоторое множество комплексных чисел (или множество точек комплексной плоскости). Пусть комплексное число 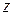 может принимать любое значение из
может принимать любое значение из 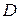 , тогда будем называть
, тогда будем называть 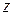 - комплексным переменным, а
- комплексным переменным, а 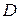 - областью его изменения.
- областью его изменения.
Определение. Величина 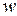 называется функцией независимого переменного
называется функцией независимого переменного 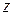 , если каждому значению
, если каждому значению 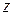 соответствует одно или несколько комплексных значений
соответствует одно или несколько комплексных значений 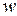 , при этом пишут:
, при этом пишут: 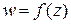 .
.
Запишем комплексные числа 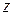 и
и 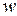 в алгебраической форме:
в алгебраической форме:
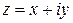 ,
, 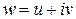 .
.
Тогда 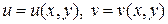 , и значит, задание функции комплексного переменного
, и значит, задание функции комплексного переменного 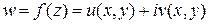 эквивалентно заданию двух действительных функций от двух действительных переменных.
эквивалентно заданию двух действительных функций от двух действительных переменных.
Определение. Число 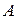 называется пределом функции
называется пределом функции 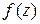 при
при 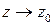 , если для любого
, если для любого 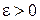 найдется такое
найдется такое 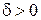 , что
, что 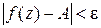 как только
как только 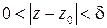 (
(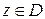 ). Записывают:
). Записывают: 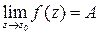 .
.
Несложно показать, что соотношение 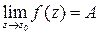 ,
,
где 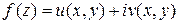 , а
, а 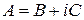 ,
, 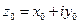 эквивалентно двум действительным соотношениям:
эквивалентно двум действительным соотношениям: 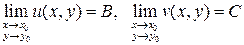 .
.
Определение. Функция 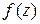 называется непрерывной в точке
называется непрерывной в точке 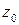 , если она определена в некоторой окрестности этой точки и
, если она определена в некоторой окрестности этой точки и 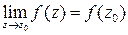 .
.
Если 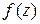 , определенная на множестве
, определенная на множестве 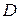 , непрерывна в каждой точке этого множества, то говорят, что она непрерывна на множестве
, непрерывна в каждой точке этого множества, то говорят, что она непрерывна на множестве 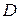 . Вновь легко показать, что условие непрерывности функции
. Вновь легко показать, что условие непрерывности функции 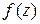 в точке
в точке 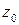 эквивалентно двум соотношениям:
эквивалентно двум соотношениям: 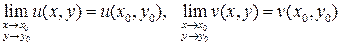 . Таким образом, функция комплексного переменного непрерывна в точке
. Таким образом, функция комплексного переменного непрерывна в точке 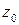 тогда и только тогда, когда ее действительная и мнимая части, рассматриваемые как функции действительных переменных
тогда и только тогда, когда ее действительная и мнимая части, рассматриваемые как функции действительных переменных 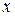 и
и 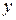 , непрерывны в той же точке.
, непрерывны в той же точке.
Введем определения основных элементарных функций комплексного переменного.
Показательная функция 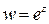 .
.
Определение. Функция 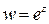 для комплексных значений z=x+iy определяется формулой:
для комплексных значений z=x+iy определяется формулой: 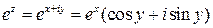 .
.
Следовательно, 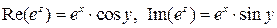
Свойства функции 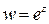 :
:
· Для любых 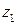 и
и 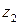 справедливо:
справедливо: 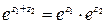 .
.
· Функция 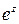 периодична с периодом
периодична с периодом 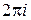 :
: 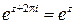 .
.
· Функция 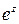 непрерывна на всей комплексной области.
непрерывна на всей комплексной области.
· Для любого 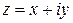 имеют место равенства:
имеют место равенства: 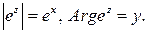
· Функция 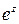 принимает все значения, кроме нуля, т.е. уравнение
принимает все значения, кроме нуля, т.е. уравнение 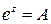 разрешимо для любого комплексного
разрешимо для любого комплексного 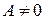 .
.
 2015-04-01
2015-04-01 19476
19476
