Тригонометрические функции комплексного аргумента определяются формулами:
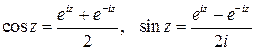 ,
, 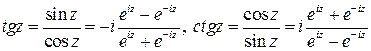 .
.
Свойства тригонометрических функций:
· функции 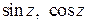 непрерывны на всей комплексной плоскости,
непрерывны на всей комплексной плоскости,
· функции 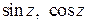 принимают все значения, т.е. уравнения
принимают все значения, т.е. уравнения 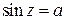 и
и 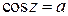 имеют решения для любого комплексного числа
имеют решения для любого комплексного числа 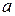 .
.
· 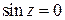 при
при 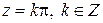 ;
; 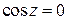 при
при 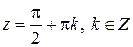 .
.
· все формулы элементарной тригонометрии, справедливые для всех действительных чисел, остаются справедливыми и при всех комплексных значениях z.
Например:
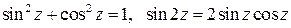 ,
,
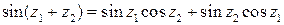 ,
,
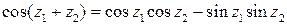 .
.
· функции 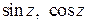 являются периодическими с периодом
являются периодическими с периодом 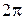 :
: 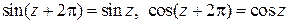
· функция 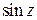 - нечетная функция,
- нечетная функция, 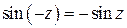 ; функция
; функция 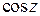 - четная функция,
- четная функция, 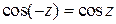 .
.
· функция 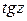 непрерывна при
непрерывна при 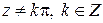 , функция
, функция 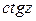 непрерывна при
непрерывна при 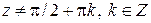 .
.
 2015-04-01
2015-04-01 1128
1128
