По функциональному ряду 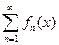 построим последовательность частичных сумм:
построим последовательность частичных сумм: 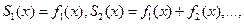
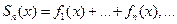
Определение. Предел последовательности частичных сумм называют суммой функционального ряда: 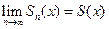 . Если при каждом
. Если при каждом 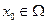 , функциональный ряд сходится, то
, функциональный ряд сходится, то 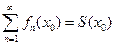 .
.
Определение. Говорят, что сходящийся функциональный ряд 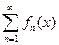 равномерно сходится на отрезке
равномерно сходится на отрезке 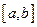 к функции
к функции 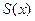 , если для
, если для 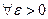 найдется не зависящий от x номер
найдется не зависящий от x номер 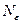 такой, что при
такой, что при 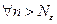 выполняется неравенство
выполняется неравенство 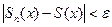 ,
, 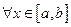 .
.
Теорема 1 (признак Вейерштрасса). Если члены ряда 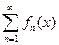 удовлетворяют неравенствам
удовлетворяют неравенствам 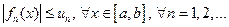 , где
, где 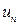 - члены сходящегося числового ряда
- члены сходящегося числового ряда 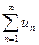 , то ряд
, то ряд 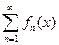 сходится на
сходится на 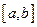 равномерно.
равномерно.
Теорема 2 (Непрерывность суммы функционального ряда). Пусть 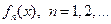 непрерывны на отрезке
непрерывны на отрезке 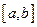 , и ряд
, и ряд 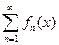 сходится на
сходится на 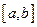 равномерно. Тогда сумма
равномерно. Тогда сумма 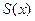 этого ряда непрерывна на
этого ряда непрерывна на 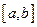 .
.
Теорема 3 (Почленный переход к пределу). Если выполнены условия теоремы 2, то для 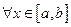 существует предел суммы функционального ряда
существует предел суммы функционального ряда 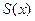 , и он равен
, и он равен 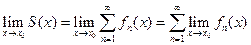 .
.
Теорема 4 (Почленное интегрирование). Пусть 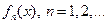 непрерывны, и пусть ряд
непрерывны, и пусть ряд 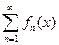 сходится на
сходится на 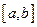 равномерно. Тогда сумма ряда интегрируема, причем
равномерно. Тогда сумма ряда интегрируема, причем 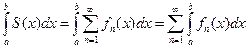 .
.
Теорема 5 (Почленное дифференцирование). Пусть 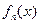 непрерывно-дифференцируемы на отрезке
непрерывно-дифференцируемы на отрезке 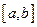 , и на этом отрезке ряды
, и на этом отрезке ряды 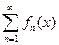 и
и 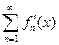 сходятся равномерно. Тогда сумма
сходятся равномерно. Тогда сумма 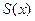 ряда
ряда 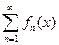 имеет на
имеет на 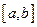 непрерывную производную, при этом
непрерывную производную, при этом 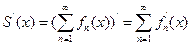 .
.
 2015-04-01
2015-04-01 3499
3499
