Предельные теоремы теории вероятностей

В теории вероятностей доказаны две группы предельных теорем. Одна из них носит название «закон больших чисел», другая – «центральная предельная теорема».

Физическое содержание закона больших чисел, понимаемого в широком смысле слова, заключается в том, что при очень большом числе случайных явлений средний их результат практически перестает быть случайным и может быть предсказан с большой степенью точности. В узком смысле слова, это группа математических теорем, в каждой из которых, для тех или иных условий, устанавливается факт приближения средних характеристик большого числа опытов к некоторым определенным постоянным.

Теорема 7 (Неравенство Чебышева, используемое для доказательства «закона больших чисел»). Вероятность того, что отклонение случайной величины от ее математического ожидания по абсолютной величине меньше положительного числа 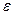, не меньше, чем 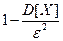, то есть

.

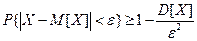Подчеркнем, что эта оценка справедлива для любого закона распределения случайной величины.

Теорема 8 (Теорема Чебышева, одна из форм «закона больших чисел»). Если случайные величины 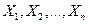попарно независимы, имеют конечные математические ожидания и дисперсии этих величин равномерно ограничены (не превышают постоянного числа 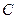), то среднее арифметическое случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий, т.е. для любого числа 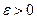выполняется неравенство 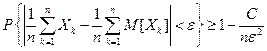, откуда

.

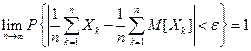Замечание. Если в условиях теоремы 8, все случайные величины имеют одно и то же математическое ожидание 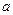: 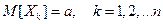, то .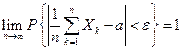

Пусть рассматривается последовательность независимых испытаний, в каждом из которых с некоторой постоянной вероятностью 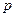наступает событие 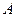(схема Бернулли).

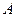Теорема 9. (Теорема Бернулли, одна из форм «закона больших чисел»). Если - число наступлений события в 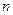независимых испытаниях и 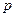- вероятность наступления события 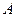в каждом из испытаний, то при любом : .

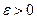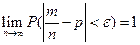«Центральная предельная теорема» это группа математических теорем, устанавливающих тот факт, что при суммировании достаточно большого числа случайных величин, закон распределения суммы неограниченно приближается к нормальному закону распределения. Условия этих теорем по существу сводятся к требованию, чтобы вклад в дисперсию всей суммы от отдельных слагаемых был равномерно малым, то есть, чтобы в состав суммы не входили члены, дисперсия которых сравнима с дисперсией всей суммы.