2015-04-01
565
Если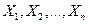 
- независимые случайные величины, имеющие одно и то же распределение с математическим ожиданием 
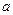и дисперсией 
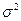, то для любого действительного 
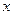, функция распределения стандартизированного среднего арифметического случайных величин сходится к функции Лапласа:
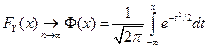, где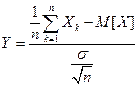 
.
Иначе, можно сказать, что, при неограниченном возрастании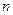 
закон распределения суммы 
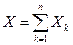неограниченно приближается к нормальному закону распределения.
Как следствия «центральной предельной теоремы», на практике широко используются, так называемые локальная и интегральная теоремы Лапласа.
Теорема 11 (Локальная теорема Лапласа). Если вероятность наступления события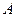 
в каждом из 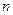независимых испытаний равна одной и той же постоянной 
(
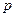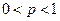), то вероятность 
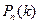того, что во всех этих испытаниях событие 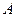наступит ровно 
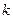раз, приближенно выражается формулой: 
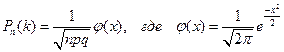, а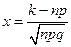 
.
Подставляя, получаем: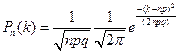 
.
Теорема 12 (Интегральная теорема Лапласа). Если вероятность наступления события 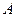в каждом из 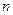независимых испытаний равна одной и той же постоянной 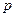(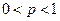), то вероятность 
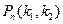того, что во всех этих испытаниях событие 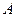наступит не менее 
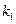раз и не более 
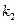раз, приближенно выражается формулой
;
, 
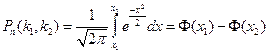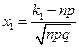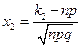, где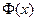 
- функция Лапласа.
Пример. Вероятность поражения мишенистрелком при одном выстреле равна 0,75. Найти вероятность того, что при 100 выстрелах мишень будет поражена не менее 70 и не более 80 раз.
Решение. Условие задачи вписывается в схему Бернулли, имеем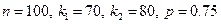 
, поэтому 
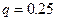. Воспользуемся теоремой 12, предварительно вычислив 
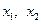по формулам: 
, 
.
.
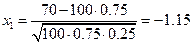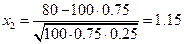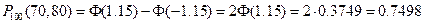В заключение этого раздела отметим, что «закон больших чисел» и «центральная предельная теорема» лежат в основе математической статистики, поскольку позволяют высказывать статистические прогнозы и оценивать точность этих прогнозов.
